【题目】在平面直角坐标系xOy中![]() 如图
如图![]() ,已知抛物线
,已知抛物线![]() ,经过点
,经过点![]() 、
、![]() .
.
(1)求此抛物线顶点C的坐标;
(2)联结AC交y轴于点D,联结BD、BC,过点C作![]() ,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.

参考答案:
【答案】(1)C(2,-3);(2)![]() .
.
【解析】试题分析:(1)已知抛物线过A,B两点,可将A,B的坐标代入抛物线的解析式中用待定系数法即可求出抛物线的解析式.然后可根据抛物线的解析式得出顶点C的坐标.
(2)分别求直线AC的解析式和BD的解析式,直线AC:y=-x-1,直线BD:y=![]() x-1,可得D和P的坐标,证明△BPG∽△CPH和△HPG∽△CPB,列比例式可得HG的长
x-1,可得D和P的坐标,证明△BPG∽△CPH和△HPG∽△CPB,列比例式可得HG的长
试题解析:(1)把A(-1,0)、B(5,0)代入抛物线解析式,
得: 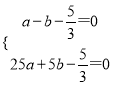 ,
,
解得: 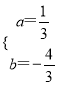 ,
,
∴抛物线的解析式为:y=![]() x2
x2![]() x
x![]() =
=![]() (x2)23,
(x2)23,
∴顶点C(2,-3)
(2)设BD与CG相交于点P,

设直线AC的解析式为:y=kx+b
把A(-1,0)和C(2,-3)代入得:
![]() ,
,
解得: ![]()
则直线AC:y=-x-1,
∴D(0,-1),
同理可得直线BD:y=![]() x-1,
x-1,
∴P(2,![]() )
)
∵∠CHP=∠PGB=90°,∠GPB=∠CPH
∴△BPG∽△CPH,
∴![]() ,
,
∴△HPG∽△CPB,
∴![]() ,
,
∴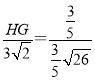 ,
,
∴HG=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,1)、B(0,﹣2)、C(1,0),点P(0,2)绕点A旋转180°得到点
 ,点
,点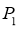 绕点B旋转180°得到点
绕点B旋转180°得到点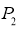 ,点
,点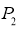 绕点C旋转180°得到点
绕点C旋转180°得到点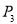 ,点
,点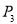 绕点A旋转180°得到点
绕点A旋转180°得到点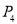 ,…,按此作法进行下去,则点
,…,按此作法进行下去,则点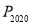 的坐标为( )
的坐标为( )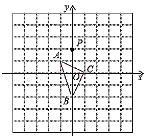
A.(0,4)B.(﹣2,0)C.(2,﹣4)D.(﹣2,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
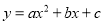 的图象上部分点的横坐标x与纵坐标y的对应值如下表:
的图象上部分点的横坐标x与纵坐标y的对应值如下表:x

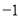
0
1
2

y

0
3
4
3

那么关于它的图象,下列判断正确的是
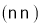
A. 开口向上 B. 与x轴的另一个交点是
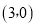
C. 与y轴交于负半轴 D. 在直线
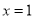 的左侧部分是下降的
的左侧部分是下降的 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
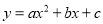 的顶点为
的顶点为 ,与x轴的一个交点A在点
,与x轴的一个交点A在点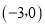 和
和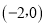 之间,其部分图象如图,其中错误的结论为
之间,其部分图象如图,其中错误的结论为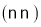
A. 方程
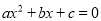 的根为
的根为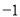 B.
B. 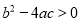
C.
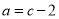 D.
D. 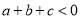
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,AE平分
 交BC于点E,且
交BC于点E,且 ,
,  ,连接OE.下列结论:①
,连接OE.下列结论:① ;②SABCD=ABAC;③OB=AB;④
;②SABCD=ABAC;③OB=AB;④ ,成立的个数有_________个.
,成立的个数有_________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式a×23-b×22-c×21+d计算出每一行的数据.第一行表示年级,第二行表示班级,如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的编号是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
(1)求证:△ACD≌△CBF;
(2)点D在线段BC上何处时,四边形CDEF是平行四边形且
 .
.
相关试题

