【题目】如图甲是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个全等的小长方形,再按图乙围成一个较大的正方形.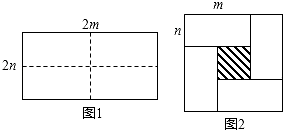
(1)请用两种方法表示图中阴影部分面积(只需表示,不必化简);
(2)比较(1)两种结果,你能得到怎样的等量关系?
请你用(2)中得到等量关系解决下面问题:如果m﹣n=5,mn=14,求m+n的值.
参考答案:
【答案】
(1)解:方法一:∵大正方形的面积为(m+n)2,四个小长方形的面积和为4mn,
∴中间阴影部分的面积为(m+n)2﹣4mn.
方法二:∵中间小正方形的边长为m﹣n,∴其面积为(m﹣n)2
(2)解:(m+n)2﹣4mn=(m﹣n)2.
∵m﹣n=5,mn=14,
∴(m+n)2﹣4×14=52,得m+n=9或m+n=﹣9(舍),
故m+n的值为9
【解析】(1)由图2的面积减去图一的面积可得阴影部分面积为(m+n)2﹣4mn;单独看图2易得阴影部分小正方形边长为m-n,可得面积为(m﹣n)2;
(2)由乘法公式易得(m+n)2﹣4mn=(m﹣n)2即两种结果相等;将m﹣n=5,mn=14带入易得m+n的值为9(边长之和为正数,所以-9舍去)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是( )
A. 抛物线开口向上
B. 抛物线的对称轴是x=1
C. 当x=1时,y的最大值为-4
D. 抛物线与x轴的交点为(-1,0),(3,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市辖区内长江流域水质情况的调查
B.对乘坐飞机的旅客是否携带违禁物品的调查
C.对一个社区每天丢弃塑料袋数量的调查
D.对重庆电视台“天天630”栏目收视率的调查 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF;
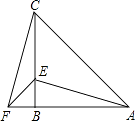
(1)求证:Rt△ABE≌Rt△CBF;
(2)求证:AB=CE+BF;
(3)若∠CAE=30°,求∠ACF度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若
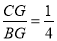 ,则
,则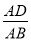 =( )
=( )
A.
 B.
B. 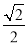 C.
C. 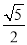 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形OABC中,OA=3,AB=6,以OA、OC所在的直线为坐标轴,建立如图所示的平面直角坐标系。将矩形OABC绕点O顺时针方向旋转,得到矩形ODEF,当点B在直线DE上时,设直线DE和
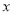 轴交于点P,与
轴交于点P,与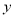 轴交于点Q.(1)求证:△BCQ≌△ODQ;(2)求点P的坐标;
轴交于点Q.(1)求证:△BCQ≌△ODQ;(2)求点P的坐标;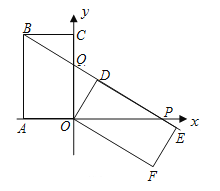
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )

A.100°
B.90°
C.80°
D.70°
相关试题

