【题目】解方程:
(1) (x-1)2=4;
(2)(x-3)2+2x(x-3)=0.
参考答案:
【答案】(1)x1=3,x2=-1;(2)x1=3,x2=1
【解析】
(1)运用直接开平方法进行解答即可;(2)运用因式分解法进行解答即可.
解:(1)(x-1)2=4
x-1=±2
x1=3,x2=-1
(2)(x-3)2+2x(x-3)=0
(x-3) (x-3+2x)=0
x1=3,x2=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】将方程5x﹣1=4x变形为5x﹣4x=1,这个过程利用的性质是( )
A. 等式性质1 B. 等式性质2
C. 移项 D. 以上说法都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年爷爷78岁,孙子24岁,(_______)年前爷爷的年龄是孙子的4倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′ , 连接AB′,并有AB′=3,则∠A′的度数为( )
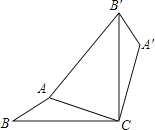
A.125°
B.130°
C.135°
D.140° -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=-x-1的图象与y轴的交点坐标为( )
A.(-1,0)B.(1,0)C.(0,1)D.(0,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
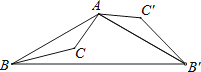
A.45°
B.60°
C.70°
D.90° -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
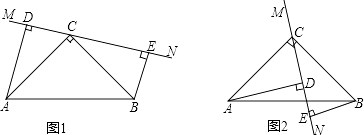
(1)当直线MN绕点C旋转到图1的位置时, 求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
相关试题

