【题目】如图,△ABC为钝角三角形,将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )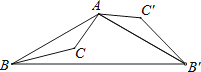
A.45°
B.60°
C.70°
D.90°
参考答案:
【答案】D
【解析】∵将△ABC绕点A按逆时针方向旋转120°得到△AB′C′,
∴∠BAB′=∠CAC′=120°,AB=AB′,
∴∠AB′B= ![]() (180°-120°)=30°,
(180°-120°)=30°,
∵AC′∥BB′,
∴∠C′AB′=∠AB′B=30°,
∴∠CAB′=∠CAC′-∠C′AB′=120°-30°=90°.
故选D.
【考点精析】本题主要考查了旋转的性质的相关知识点,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′ , 连接AB′,并有AB′=3,则∠A′的度数为( )
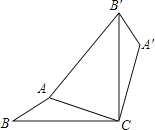
A.125°
B.130°
C.135°
D.140° -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1) (x-1)2=4;
(2)(x-3)2+2x(x-3)=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=-x-1的图象与y轴的交点坐标为( )
A.(-1,0)B.(1,0)C.(0,1)D.(0,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
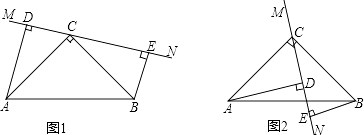
(1)当直线MN绕点C旋转到图1的位置时, 求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE , 若∠CAE=65°,∠E=70°,且AD⊥BC , 则∠BAC的度数为( )
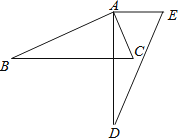
A.60°
B.85°
C.75°
D.90° -
科目: 来源: 题型:
查看答案和解析>>【题目】A城有某种农机30台,B城有该农机40台,现要将这些农机全部运往C,D两乡,调运任务承包给某运输公司.已知C乡需要农机34台,D乡需要农机36天,从A城往C,D两乡运送农机的费用分别为250元/台和200元/台,从B城往C,D两乡运送农机的费用分别为150元/台和240元/台.
(1)设A城运往C乡该农机x台,运送全部农机的总费用为W元,求W关于x的函数关系式,并写出自变量x的取值范围;
(2)现该运输公司要求运送全部农机的总费用不低于16460元,则有多少种不同的调运方案?将这些方案设计出来;
(3)现该运输公司决定对A城运往C乡的农机,从运输费中每台减免a元(a≤200)作为优惠,其它费用不变,如何调运,使总费用最少?
相关试题

