【题目】如图,大楼外墙有高为AB的广告牌,由距离大楼20米的点C(即CD=20米)观察它的顶部A的仰角是55°,底部B的仰角是42°。求AB的高度.(结果精确到整数)
(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,)

参考答案:
【答案】AB的高度为10.6m.
【解析】试题分析:由题意可得:∠ACD=55°,∠BCD=42°,CD=20,在直角三角形中由tan∠ACD=![]() ,tan∠BCD=
,tan∠BCD=![]() 可求出AD和BD 的长度,再根据AB=AD-BD即可;
可求出AD和BD 的长度,再根据AB=AD-BD即可;
试题解析:
由已知可得:∠ACD=55°,∠BCD=42°,CD=20,
又∵tan∠ACD=![]() ,tan∠BCD=
,tan∠BCD=![]() ,
,
∴AD=CDtan∠ACD,BD=CDtan∠BCD,
∴AB=AD-BD=CDtan∠ACD-CDtan∠BCD
≈20×1.43-20×0.90
≈10.6(m)
答:AB的高度为10.6m。
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
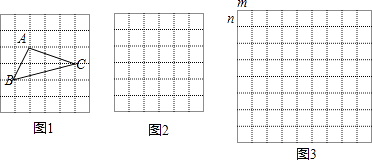
(1)在△ABC中,AB、BC、AC三边的长分别为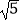 、
、 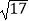 、
、 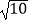 ,求这个三角形的面积. 如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC的高,而借用网格就能就算出它的面积.
,求这个三角形的面积. 如图1,某同学在解答这道题时,先建立一个每个小正方形的边长都是1的网格,再在网格中画出边长符合要求的格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),这样不需要求△ABC的高,而借用网格就能就算出它的面积.
请你将△ABC的面积直接填写在横线上 .
(2)思维拓展: 已知△ABC三边的长分别为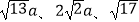 a(a>0),求这个三角形的面积.
a(a>0),求这个三角形的面积.
我们把上述求△ABC面积的方法叫做构图法.如图2,网格中每个小正方形的边长都是a,请在网格中画出相应的△ABC,并求出它的面积.
(3)类比创新: 若△ABC三边的长分别为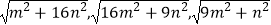 (m>0,n>0,且m≠n),求出这个三角形的面积.
(m>0,n>0,且m≠n),求出这个三角形的面积.
如图3,网格中每个小长方形长、宽都是m,n,请在网格中画出相应的△ABC,用网格计算这个三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列叙述,其中不正确的是( )
A. 过一点有且只有一条直线与已知直线平行 B. 同角(或等角)的余角相等
C. 两点确定一条直线 D. 两点之间的所有连线中,线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x<6的非负整数解为( )
A.0,1,2 B.1,2 C.0,-1,-2 D.无数个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC的中点为D,BC的中点为E,F是DE的中点,动点G在边AB上,连接GF,延长GF到点H,使HF=GF,连接HD,HE.
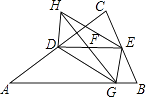
(1)求证:四边形HDGE是平行四边形.
(2)已知∠C=90°,∠A=30°,AB=4.
①当AG为何值时,四边形HDGE是矩形;
②当AG为何值时,四边形HDGE是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式x+3≤6的正整数解为___________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣1,﹣2,0,1四个数中最小的数是( )
A.﹣1
B.﹣2
C.0
D.1
相关试题

