【题目】(模型建立)
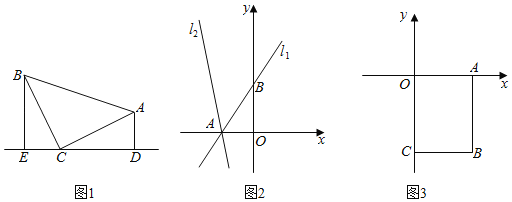
(1)如图1,等腰Rt△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,求证:△BEC≌△CDA;
(模型应用)
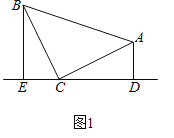
(2)如图2,已知直线l1:y=![]() x+3与x轴交于点A,与y轴交于点B,将直线l1绕点A逆时针旋转45°至直线l2;求直线l2的函数表达式;
x+3与x轴交于点A,与y轴交于点B,将直线l1绕点A逆时针旋转45°至直线l2;求直线l2的函数表达式;
(3)如图3,平面直角坐标系内有一点B(3,﹣4),过点B作BA⊥x轴于点A、BC⊥y轴于点C,点P是线段AB上的动点,点D是直线y=﹣2x+1上的动点且在第四象限内.试探究△CPD能否成为等腰直角三角形?若能,求出点D的坐标,若不能,请说明理由.
参考答案:
【答案】(1)见详解;(2)![]() ;(3)点D坐标得(
;(3)点D坐标得(![]() ,
,![]() )或(4,
)或(4,![]() 7)或(
7)或(![]() ,
,![]() ).
).
【解析】
(1)由垂直的定义得∠ADC=∠CEB=90°,平角的定义和同角的余角的相等求出∠DAC=∠ECB,角角边证明△CDA≌△BEC;
(2)证明△ABO≌∠BCD,求出点C的坐标为(-3,5),由点到直线上构建二元一次方程组求出k=![]() 5,b=
5,b=![]() 10,待定系数法求出直线l2的函数表达式为y=-5x-10;
10,待定系数法求出直线l2的函数表达式为y=-5x-10;
(3)构建△MCP≌△HPD,由其性质,点D在直线y=-2x+1求出m=![]() 或n=0或
或n=0或![]() ,将m的值代入,得点D坐标得(
,将m的值代入,得点D坐标得(![]() ,
,![]() )或(4,
)或(4,![]() 7)或(
7)或(![]() ,
,![]() ).
).
解:(1)如图1所示:
∵AD⊥ED,BE⊥ED,
∴∠ADC=∠CEB=90°,
又∵∠ACD+∠ACB+∠BEC=180°,∠ACB=90°,
∴∠ACD+∠BEC=90°,
又∵∠ACD+∠DAC=90°,
∴∠DAC=∠ECB,
在△CDA和△BEC中,
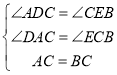 ,
,
∴△CDA≌△BEC(AAS);
(2)过点B作BC⊥AB交AC于点C,CD⊥y轴交y轴于点D,如图2所示:
∵CD⊥y轴,x轴⊥y轴,
∴∠CDB=∠BOA=90°,
又∵BC⊥AB,
∴∠ABC=90°,
又∵∠ABO+∠ABC+∠CBD=180°,
∴∠ABO+∠CBD=90°,
又∵∠BAO+∠ABO=90°,
∴∠BAO=∠CBD,
又∵∠BAC=45°,
∴∠ACB=45°,
∴AB=CB,
在△ABO和∠BCD中,
 ,
,
∴△ABO≌∠BCD(AAS),
∴AO=BD,BO=CD,
又∵直线l1:y=![]() x+3与x轴交于点A,与y轴交于点B,
x+3与x轴交于点A,与y轴交于点B,
∴点A、B两点的坐标分别为(-2,0),(0,3),
∴AO=2,BO=3,
∴BD=2,CD=3,
∴点C的坐标为(-3,5),
设l2的函数表达式为y=kx+b(k≠0),
点A、C两点在直线l2上,依题意得:
![]() ,
,
∴![]() ,
,
∴直线l2的函数表达式为y=![]() 5x
5x![]() 10;
10;
(3)能成为等腰直角三角形,依题意得,
①若点P为直角时,如图3甲所示:
设点P的坐标为(3,m),则PB的长为4+m,
∵∠CPD=90°,CP=PD,
∠CPM+∠CDP+∠PDH=180°,
∴∠CPM+∠PDH=90°,
又∵∠CPM+∠DPM=90°,
∴∠PCM=∠PDH,
在△MCP和△HPD中,
 ,
,
∴△MCP≌△HPD(AAS),
∴CM=PH,PM=PD,
∴点D的坐标为(7+m,-3+m),
又∵点D在直线y=-2x+1上,
∴-2(7+m)+1=-3+m,
解得:m=![]() ,
,
即点D的坐标为(![]() ,
,![]() );
);
②若点C为直角时,如图3乙所示:
设点P的坐标为(3,n),则PB的长为4+n,
CA=CD,
同理可证明△PCM≌△CDH(AAS),
∴PM=CH,MC=HD,
∴点D的坐标为(4+n,-7),
又∵点D在直线y=-2x+1上,
∴-2(4+n)+1=-7,
解得:n=0,
∴点P与点A重合,点M与点O重合,
即点D的坐标为(4,-7);
③若点D为直角时,如图3丙所示: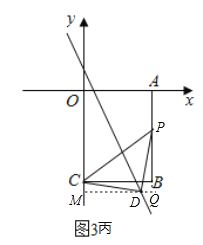
设点P的坐标为(3,k),则PB的长为4+k,
CD=PD,
同理可证明△CDM≌△PDQ(AAS),
∴MD=PQ,MC=DQ,
∴点D的坐标为(![]() ,
,![]() ),
),
又∵点D在直线y=-2x+1上,
∴-2×![]() +1=
+1=![]() ,
,
解得:k=![]() ,
,
∴点P与点A重合,点M与点O重合,
即点D的坐标为(![]() ,
,![]() );
);
综合上述,点D坐标得(![]() ,
,![]() )或(4,
)或(4,![]() 7)或(
7)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如果
 +(n+6)2=0,求(m+n)2008+m3的值
+(n+6)2=0,求(m+n)2008+m3的值(2)已知实数a,b,c,d,e,且ab互为倒数,c,d互为相反数,e的绝对值为2,求
 ×ab+
×ab+ +e的值
+e的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(结果保留π)
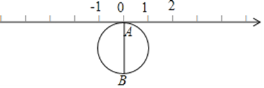
(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年新型冠状病毒肺炎疫情肆虐,红星社区为了提高社区居民的身体素质,鼓励居民在家锻炼,特采购了一批跳绳免费发放,已知2根幸福牌跳绳和1根平安牌跳绳共需31元,2根平安牌跳绳和3根幸福牌跳绳共需54元.
(1)求幸福牌跳绳和平安牌跳绳的单价;
(2)已知该社区需要采购两种品牌的跳绳共60根,且平安牌跳绳的数量不少于幸福牌跳绳数量的2倍,请设计出最省钱的购买方案,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=
 AC,连接CE、OE,连接AE,交OD于点F,若AB=2,∠ABC=600,则AE的长为( )
AC,连接CE、OE,连接AE,交OD于点F,若AB=2,∠ABC=600,则AE的长为( )
A.
 B.
B. 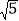 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家实行一系列“三农”优惠政策后,农民收入大幅度增加.某乡所辖村庄去年的年人均收入(单位:元)情况如下表:
年人均收入
3 500
3 700
3 800
3 900
4 500
村庄个数
1
1
3
3
1
该乡去年各村庄年人均收入的中位数是( )
A.3 700元B.3 800元C.3 850元D.3 900元
-
科目: 来源: 题型:
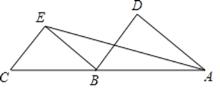
查看答案和解析>>【题目】已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,
(1)求证:BD∥CE;
(2)若∠C=70°,∠DAC=50°,求∠DBE的度数.
相关试题

