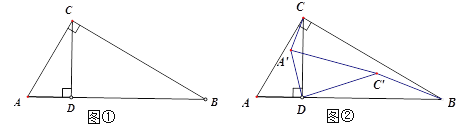
【题目】如图①,在Rt△ABC中,∠C=90°, ∠B=30°,AC=1,CD⊥AB,垂足为D,现将△ACD绕D点顺时针旋转![]() 得到△A‘C’D, 旋转时间为t秒,△ACD绕D点旋转的角速度
得到△A‘C’D, 旋转时间为t秒,△ACD绕D点旋转的角速度![]() /秒(每秒转10度) .
/秒(每秒转10度) .
(1)旋转时间t= 秒时,A‘C’∥AB;
(2)△ACD绕D点顺时针旋转一周(3600),斜边AC扫过的面积为 ;
(3)如图②,连接A’C、 C’B.
①若6<t<9,求证: ![]() 为定值;
为定值;
②当t>9时,上述结论还成立吗?如成立直接写出比值,不成立请说明理由.
参考答案:
【答案】(1)6(2)![]() (3)①证明见解析;②结论成立,比值仍为
(3)①证明见解析;②结论成立,比值仍为![]() .
.
【解析】分析:(1)由旋转的旋转可得若要![]() ∥AB,可
∥AB,可![]() ,即可求解;(2)由题意可知斜边AC扫过的面积为以点D为圆心CD,AC边上的高为半径的环形,利用大圆面积减去小圆面积即可求解;(3)①当6<t<9时,知60°<α<90°,由△
,即可求解;(2)由题意可知斜边AC扫过的面积为以点D为圆心CD,AC边上的高为半径的环形,利用大圆面积减去小圆面积即可求解;(3)①当6<t<9时,知60°<α<90°,由△![]() ∽△
∽△![]() 和△
和△![]() ∽△
∽△![]() 得到
得到![]() 为定值
为定值![]() ;②用与①相同的方法即可得出结果.
;②用与①相同的方法即可得出结果.
本题解析:
(1)由![]() ∥AB,得
∥AB,得![]() ,∴t=6.
,∴t=6.
(2)设AC边上的高为h,由![]() .
.
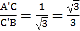
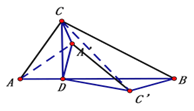
(3)①当6<t<9时,知600<![]() <900
<900
如图连接AA‘、C C’
由旋转定义知
∠AD A‘=∠CD C’=∠![]()
∵AD=A‘D、CD= C‘D
∴△ADA‘ ∽△C D C‘.
∴∠A‘A D =∠C‘CD ; ![]() ,
,
又∵∠CAD =∠BCD =60O
∴△ACA‘ ∽△C BC’
∴![]() 为定值.
为定值.
②结论成立,比值仍为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式因式分解:(1)4x2-8x+4;(2)(x+y)2-4y(x+y)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 是最大的负整数,
是最大的负整数, 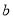 是最小的正整数,且
是最小的正整数,且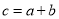 ,请回答下列问题:
,请回答下列问题:(
 )请直接写出
)请直接写出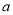 ,
, 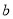 ,
, 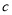 的值,
的值, 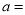 __________;
__________; 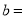 __________;
__________; 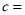 __________.
__________.(
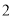 )
)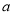 ,
, 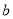 ,
, 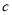 在数轴上所对应的点分别为
在数轴上所对应的点分别为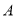 ,
, 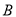 ,
, 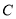 ,请在数轴上表示
,请在数轴上表示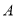 ,
, 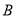 ,
, 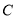 三点.
三点.(
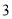 )在(
)在(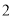 )的情况下,点
)的情况下,点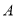 ,
, 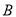 ,
, 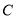 开始在数轴上运动,若点
开始在数轴上运动,若点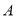 、点
、点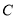 都以每秒
都以每秒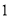 个单位的速度向左运动,同时,点
个单位的速度向左运动,同时,点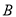 以每秒
以每秒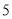 个单位长度的速度向右运动,假设
个单位长度的速度向右运动,假设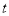 秒过后,若点
秒过后,若点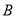 与点
与点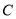 之间的距离表示为
之间的距离表示为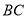 ,点
,点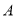 与点
与点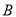 之间的距离表示为
之间的距离表示为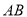 .请问
.请问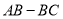 的值是否随着时间
的值是否随着时间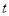 的变化而变化?若变化,请说明理由;若不变,请求出
的变化而变化?若变化,请说明理由;若不变,请求出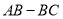 的值.
的值.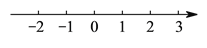
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据2,3,x,5,7的平均数是4,则这组数据的众数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】算式(3.0×106)(5.0×10﹣3)的结果用科学记数法表达正确的是( )
A.15×103
B.15×104
C.1.5×103
D.1.5×104 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(3x+4y)2-(4y-3x)(3x+4y)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的个数有( )
①一元二次方程的一般形式为ax2+bx+c=0
②平分弦的直径垂直于弦,并且平分弦所对的两条弧.
③同弦或等弦所对的圆周角相等
④方程x2=x的解是x=1.
A.0B.1C.2D.3
相关试题

