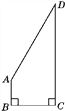
【题目】某校一块空地被荒废,如图,为了绿化环境,学校打算利用这块空地种植花草,已知AB⊥BC,CD⊥BC,AB=![]() CD=
CD=![]() m,BC=3
m,BC=3![]() m,试求这块空地的面积.
m,试求这块空地的面积.
参考答案:
【答案】![]() (m2)
(m2)
【解析】试题分析:过点A作AE⊥DC于点E,根据AB=![]() CD=
CD=![]() m即可求出DE、CD的值,进而利用勾股定理求出AD的值;根据矩形以及直角三角形的面积公式以及周长的计算方法,即可解决.
m即可求出DE、CD的值,进而利用勾股定理求出AD的值;根据矩形以及直角三角形的面积公式以及周长的计算方法,即可解决.
试题解析:过点A作AE⊥DC于点E,如图所示.
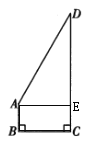
∵AB=![]() CD=
CD=![]() m,AE⊥CD,
m,AE⊥CD,
∴CD=4![]() m ,DE=3
m ,DE=3![]() m,
m,
∵AB⊥BC,CD⊥BC ,AE⊥CD, BC=3![]() m,
m,
∴四边形ABCE为矩形,
∴AE=BC=3![]() m,
m,
∵AE=3![]() m ,DE=3
m ,DE=3![]() m,
m,
∴AD=6![]() m,
m,
∵四边形ABCE为矩形,△AED为直角三角形,
∴空地的周长=AB+BC+CD+AD=9![]() +5
+5![]() (m)
(m)
空地的面积=AB·BC+![]() AE·DE=15
AE·DE=15![]() (m3).
(m3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】要把一根木条在墙上钉牢,至少需要枚钉子.其中的道理是
-
科目: 来源: 题型:
查看答案和解析>>【题目】一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则一次性购买盒子所需要最少费用为 元.
型号
A
B
单个盒子容量(升)
2
3
单价(元)
5
6
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式x﹣b≥0恰有两个负整数解,则b的取值范围是( )
A.﹣3<b<﹣2
B.﹣3<b≤﹣2
C.﹣3≤b≤﹣2
D.﹣3≤b<﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣p)2(﹣p)3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将饰品售价调整为60+x(元/件)(x>0即售价上涨,x<0即售价下降),每月饰品销量为y(件),月利润为w(元).
(1)直接写出y与x之间的函数关系式;
(2)如何确定销售价格才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元应如何控制销售价格?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2
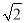 =(1+
=(1+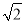 )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:设a+b
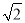 =(m+n
=(m+n )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b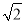 =m2+2n2+2mn
=m2+2n2+2mn .
.∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b
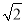 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b
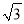 =
=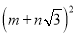 ,用含m、n的式子分别表示a、b,得:a=__,b=__;
,用含m、n的式子分别表示a、b,得:a=__,b=__;(2)利用所探索的结论,找一组正整数a、b、m、n填空:__+__
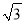 =(___)+__
=(___)+__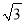 )2;
)2;(3)若a+4
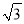 =
= ,且a、m、n均为正整数,求a的值?
,且a、m、n均为正整数,求a的值?
相关试题

