【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
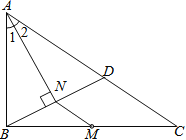
(1)求证:BN=DN;
(2)求△ABC的周长
参考答案:
【答案】解:∵三角形ABCD是矩形.
∴∠ABC=∠BCD=90°.
∵△PBC和△QCD是等边三角形.
∴∠PBC=∠PCB=∠QCD=60°.
∴∠PBA=∠ABC-∠PBC=30°,
∠PCD=∠BCD-∠PCB=30°.
∴∠PCQ=∠QCD-∠PCD=30°.
∴∠PBA=∠PCQ=30°.
【解析】试题分析:(1)证明△ABN≌△ADN,即可得出结论;
(2)先判断MN是△BDC的中位线,从而得出CD,由(1)可得AD=AB=10,从而计算周长即可.
(1)证明:在△ABN和△ADN中,
∵![]() ,
,
∴△ABN≌△ADN(ASA),
∴BN=DN.
(2)解:∵△ABN≌△ADN,
∴AD=AB=10,
又∵点M是BC中点,
∴MN是△BDC的中位线,
∴CD=2MN=6,
故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
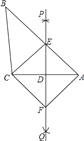
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实优秀传统文化进校园,某校计划购进“四书”、“五经”两套图书供学生借阅,已知这两套图书单价和为660元,一套“四书”比一套“五经”的2倍少60元.
(1)分别求出这两套图书的单价;
(2)该校购买这两套图书不超过30600元,且购进“四书”至少33套,“五经”的套数是“四书”套数的2倍,该校共有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索新知:
如图1,射线OC在
 的内部,图中共有3个角:
的内部,图中共有3个角: ,
, 和
和 ,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是
,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是 的“巧分线”.
的“巧分线”.(1)一个角的平分线______这个角的“巧分线”;
 填“是”或“不是”
填“是”或“不是”
(2)如图2,若
 ,且射线PQ是
,且射线PQ是 的“巧分线”,则
的“巧分线”,则 ______;
______; 用含
用含 的代数式表示出所有可能的结果
的代数式表示出所有可能的结果
深入研究:
如图2,若
 ,且射线PQ绕点P从PN位置开始,以每秒
,且射线PQ绕点P从PN位置开始,以每秒 的速度逆时针旋转,当PQ与PN成
的速度逆时针旋转,当PQ与PN成 时停止旋转,旋转的时间为t秒.
时停止旋转,旋转的时间为t秒.(3)当t为何值时,射线PM是
 的“巧分线”;
的“巧分线”;(4)若射线PM同时绕点P以每秒
 的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是
的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是 的“巧分线”时t的值.
的“巧分线”时t的值.


-
科目: 来源: 题型:
查看答案和解析>>【题目】某区举办科技比赛,某校参加科技比赛(包括电子百拼、航模、机器人、建模四个类别)的参赛人数统计图如图
(1)该校参加机器人比赛的人数是_____人;“航模”所在扇形的圆心角度数是________°;
(2)补全条形统计图;
(3)从全区参加科技比赛选手中随机抽取80人,其中有16人获奖.今年全区参加科技比赛人数共有3215人,请你估算全区参加科技比赛的获奖人数约是多少人?

-
科目: 来源: 题型:
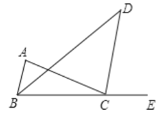
查看答案和解析>>【题目】如图,AC、BD相交于点O,∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,点E在BC的延长线上。
(1)求证:CD∥AB;
(2)若∠D=38°,求∠ACE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=10,D是BC的中点,将△ABD绕点A旋转后得到△ACE,则线段DE的长度为 .

相关试题

