【题目】如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
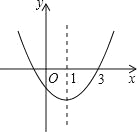
A.4ac﹣b2<0 B.a﹣b+c<0 C.2a+b<0 D.abc<0
参考答案:
【答案】B.
【解析】
试题解析:∵抛物线与x轴有两个交点,
∴b2-4ac>0,即b2>4ac,所以A选项错误;
∵抛物线开口向上,
∴a>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴ac<0,所以B选项错误;
∵二次函数图象的对称轴是直线x=1,
∴-![]() =1,∴2a+b=0,所以C选项错误;
=1,∴2a+b=0,所以C选项错误;
∵抛物线过点A(3,0),二次函数图象的对称轴是x=1,
∴抛物线与x轴的另一个交点为(-1,0),
∴a-b+c=0,所以B选项正确;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形具有而矩形不具有的性质是( )
A. 对角线垂直B. 对角线相等C. 对角线互相平分且相等D. 对角线互相平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠C=90° , a:b=3:4,运用计算器计算,∠A的度数(精确到1°)( )
A.30°
B.37°
C.38°
D.39° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个直角三角形的两条直角边的长恰好是方程x2-3x=4(x-3)的两个实数根,则该直角三角形斜边上的中线长是( )
A.3
B.4
C.6
D.2.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
交通方式 频数(人数) 频率
公共汽车 m 0.25
小车 24 0.20
摩托车 36 n
自行车 18 0.15
其它 12 0.10
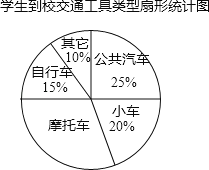
请根据图表信息解答下列问题:
(1)本次共抽样调查 个学生;
(2)填空:频数分布表中的m= ,n= ;
(3)在扇形统计图中,请计算出“摩托车”所在的扇形的圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
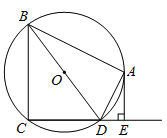
(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D是线段BC的中点,分别以点B,C为圆心, BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
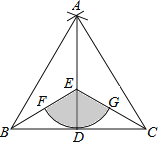
(1)求证:BE=CE;
(2)以点E为圆心,ED长为半径画弧,分别交BE,CE于点F, G.若BC=4,EB平分∠ABC,求图中阴影部分(扇形)的面积.
相关试题

