【题目】
![]()
(1)OA= cm,OB= cm.
(2)若点C是线段AO上一点,且满足AC=CO+CB,求CO的长.
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为t(s),当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP﹣OQ=8.
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后立即返回,又以同样的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程为 cm.
参考答案:
【答案】(1)16,8;(2)CO=![]() ;(3)①t=
;(3)①t=![]() 或16s时,2OP﹣OQ=8.②48cm.
或16s时,2OP﹣OQ=8.②48cm.
【解析】试题分析:(1)由OA=2OB,OA+OB=24即可求出OA、OB.
(2)设OC=x,则AC=16﹣x,BC=8+x,根据AC=CO+CB列出方程即可解决.
(3)①分两种情形①当点P在点O左边时,2(16﹣2t)﹣(8+t)=8,当点P在点O右边时,2(2t﹣16)﹣(8+x)=8,解方程即可.
②点M运动的时间就是点P从点O开始到追到点Q的时间,设点M运动的时间为ts由题意得:t(2﹣1)=16由此即可解决.
解:(1)∵AB=24,OA=2OB,
∴20B+OB=24,
∴OB=8,0A=16,
故答案分别为16,8.
(2)设CO=x,则AC=16﹣x,BC=8+x,
∵AC=CO+CB,
∴16﹣x=x+8+x,
∴x=![]() ,
,
∴CO=![]() .
.
(3)①当点P在点O左边时,2(16﹣2t)﹣(8+t)=8,t=![]() ,
,
当点P在点O右边时,2(2t﹣16)﹣(8+t)=8,t=16,
∴t=![]() 或16s时,2OP﹣OQ=8.
或16s时,2OP﹣OQ=8.
②设点M运动的时间为ts,由题意:t(2﹣1)=16,t=16,
∴点M运动的路程为16×3=48cm.
故答案为48cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
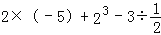
(2)
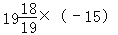
(3)
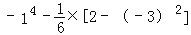
(4)
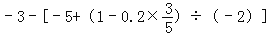
(5)
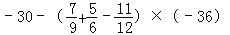 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形A1B1C1D1,黏合部分的长度为4cm.若长为30cm,宽为10cm的长方形白纸条共有100张,则小明应分配到 张长方形白纸条,才能使小明和小慧按各自要求黏合起来的长方形面积相等(要求100张长方形白纸条全部用完).
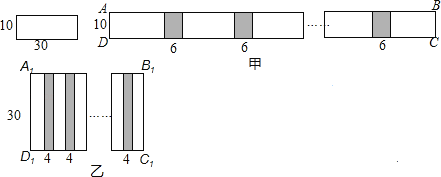
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:
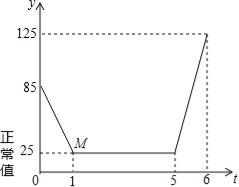
(1)写出题中的变量;
(2)写出点M的实际意义;
(3)求第1小时内,y与t的一次函数表达式;
(4)已知第5﹣6小时是小强妈妈做晚餐的时间,厨房内油烟导致PM2.5浓度升高.若该净化器吸收PM2.5的速度始终不变,则第6小时之后,预计经过多长时间室内PM2.5浓度可恢复正常?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在0、-1,1,-0.1,2,-3这六个数中中,最小的数是( )
A. 0 B. -0.1 C. -1 D. -3
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).
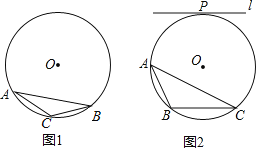
(1)如图1,AC=BC;
(2)如图2,直线l与⊙O相切于点P,且l∥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:x2+4x﹣1=0;
(2)求抛物线y=﹣x2+4x+3的顶点坐标.
相关试题

