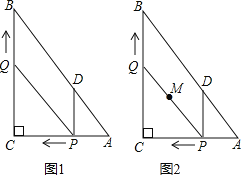
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作
,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作![]() ,交AB于点D,连接PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒
,交AB于点D,连接PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒![]() .
.
![]() 直接用含t的代数式分别表示:
直接用含t的代数式分别表示:![]() ______,
______,![]() ______;
______;
![]() 是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由.
是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由.
![]() 如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)详见解析;(3)2
;(2)详见解析;(3)2![]()
【解析】
![]() 由根据路程等于速度乘以时间可得,
由根据路程等于速度乘以时间可得,![]() ,
,![]() ,则
,则![]() ,根据
,根据![]() ,
,![]() ,可得:
,可得:![]() ,根据相似三角形的判定可得:
,根据相似三角形的判定可得:![]() ∽
∽![]() ,再根据相似三角形的性质可得:
,再根据相似三角形的性质可得:
![]() ,即
,即![]() ,从而解得:
,从而解得:![]() ,
,
(2)根据![]() ,当
,当![]() 时,可判定四边形PDBQ为平行四边形,根据平行四边形的性质可得:
时,可判定四边形PDBQ为平行四边形,根据平行四边形的性质可得:![]() ,解得:
,解得:![]() ,
,
(3)根据题意可得:![]() ,当
,当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,当
,当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的解析式为:
的解析式为:![]() ,则
,则![]() ,解得:
,解得:![]() ,因此直线
,因此直线![]() 的解析式为:
的解析式为:![]() ,再根据题意得:点P的坐标为
,再根据题意得:点P的坐标为![]() ,点Q的坐标为
,点Q的坐标为![]() ,因此在运动过程中PQ的中点M的坐标为
,因此在运动过程中PQ的中点M的坐标为![]() ,当
,当![]() 时,
时,![]() ,因此点M在直线
,因此点M在直线![]() 上,作
上,作![]() 轴于N,则
轴于N,则![]() ,
,![]() ,由勾股定理得,
,由勾股定理得,![]() ,
,
因此线段PQ中点M所经过的路径长为![]() .
.
![]() 由题意得,
由题意得,![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,即
,即![]() ,
,
解得:![]() ,
,
故答案为:![]() ,
,![]() ,
,
![]() 存在,
存在,
![]() ,
,
![]() 当
当![]() 时,四边形PDBQ为平行四边形,
时,四边形PDBQ为平行四边形,
![]() ,
,
解得:![]() ,
,
则当![]() 时,四边形PDBQ为平行四边形,
时,四边形PDBQ为平行四边形,
![]() 以点C为原点,以AC所在的直线为x轴,建立如图2所示的平面直角坐标系,
以点C为原点,以AC所在的直线为x轴,建立如图2所示的平面直角坐标系,
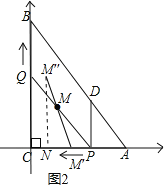
由题意得:![]() ,
,
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,
,
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,
,
设直线![]() 的解析式为:
的解析式为:![]() ,
,
则![]() ,
,
解得:![]() ,
,
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ,
,
由题意得:点P的坐标为![]() ,点Q的坐标为
,点Q的坐标为![]() ,
,
![]() 在运动过程中PQ的中点M的坐标为
在运动过程中PQ的中点M的坐标为![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点M在直线
点M在直线![]() 上,
上,
作![]() 轴于N,
轴于N,
则![]() ,
,![]() ,
,
由勾股定理得,![]() ,
,
![]() 线段PQ中点M所经过的路径长为
线段PQ中点M所经过的路径长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购买一批单价为20元的日用品,如果以单价30元销售,那么半月内可以售出400件.据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高一元,销售量相应减少20件.如何提高销售价,才能在半月内获得最大利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
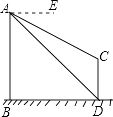
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号). -
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.

(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是形时,四边形OBEC是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=
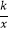 (k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点. 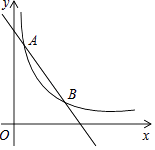
(1)求反比例函数的表达式;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;
(3)求△PAB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD,点G在AB边上,点H在BC边上,连接GH,将∠CHG对折,点C落在直线HG上的点C′处,点D落在点D′处,得到折痕FH,C′D′与AD边交于点E
(1)如果∠CHF=80°,那么∠BHG的度数是多少?
(2)如果∠DFH=110°,那么∠D′FE的度数是多少?

相关试题

