【题目】如图,长方形纸片ABCD,点G在AB边上,点H在BC边上,连接GH,将∠CHG对折,点C落在直线HG上的点C′处,点D落在点D′处,得到折痕FH,C′D′与AD边交于点E
(1)如果∠CHF=80°,那么∠BHG的度数是多少?
(2)如果∠DFH=110°,那么∠D′FE的度数是多少?

参考答案:
【答案】(1)20°(2)40°
【解析】
1)根据折叠的性质得到∠CHF=∠C′HF=80°,根据平角的定义即可得到结论;
(2)由折叠的性质得到∠D′FH=∠DFH=110°,根据平角的定义得到∠EFH=180°﹣∠DFH=70°,于是得到结论.
(1)∵将∠CHG对折,点C落在直线HG上的点C′处,
∴∠CHF=∠C′HF=80°,
∴∠BHG=180°﹣∠GHF﹣∠CHF=20°;
(2)∵将∠CHG对折,点D落在点D′处,
∴∠∠D′FH=∠DFH=110°,
∵∠EFH=180°﹣∠DFH=70°,
∴∠D′FE=∠D′FH﹣∠AFH=40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
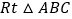 中,
中,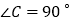 ,
,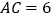 ,
,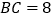 ,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作
,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作 ,交AB于点D,连接PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒
,交AB于点D,连接PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒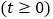 .
.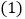 直接用含t的代数式分别表示:
直接用含t的代数式分别表示: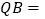 ______,
______,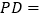 ______;
______;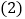 是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由.
是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由.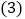 如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.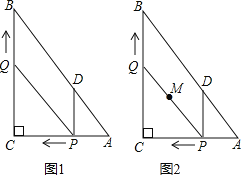
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.

(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是形时,四边形OBEC是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=
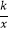 (k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点. 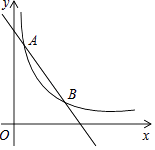
(1)求反比例函数的表达式;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;
(3)求△PAB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
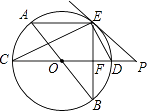
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰RtABC 中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为8cm2,则△BPC的面积为( )

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,点E在BC的延长线上,
,点E在BC的延长线上,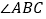 的平分线BD与
的平分线BD与 的平分线CD相交于点D,连接AD,则下列结论中,正确的是
的平分线CD相交于点D,连接AD,则下列结论中,正确的是


A.
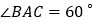 B.
B. 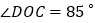 C.
C. 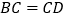 D.
D. 
相关试题

