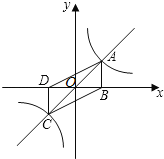
【题目】如图,正比例函数y=x与反比例函数y=![]() 的图象相交于A,C两点,AB⊥x轴于B,CD⊥x轴于D,则四边形ABCD的面积为 .
的图象相交于A,C两点,AB⊥x轴于B,CD⊥x轴于D,则四边形ABCD的面积为 .
参考答案:
【答案】2
【解析】
试题分析:首先根据反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=![]() |k|,得出S△AOB=S△ODC=
|k|,得出S△AOB=S△ODC=![]() ,再根据反比例函数的对称性可知:OB=OD,得出S△ADB+S△BDC得出结果.
,再根据反比例函数的对称性可知:OB=OD,得出S△ADB+S△BDC得出结果.
解:根据反比例函数的对称性可知:OB=OD,AB=CD,
∵四边形ABCD的面积等于S△ADB+S△BDC,
∵A(1,1),B(1,0),C(﹣1,﹣1),D(﹣1,0)
∴S△ADB=![]() (DO+OB)×AB=
(DO+OB)×AB=![]() ×2×1=1,
×2×1=1,
S△BDC=![]() (DO+OB)×DC=
(DO+OB)×DC=![]() ×2×1=1,
×2×1=1,
∴四边形ABCD的面积=2.
故答案为:2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m是关于x的方程x2﹣2x﹣3=0的一个根,则2m2﹣4m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多边形的边数由3增加到n(n为大于3的整数),则其外角和的度数( )
A. 增加 B. 减少 C. 不变 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2a﹣1)x+5﹣a=ax+1的一次项系数为4,则常数项为: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x﹣3)2+1的顶点坐标是( )
A.(3,1) B.(4,﹣1)
C.(﹣3,1) D.(﹣3,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与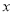 轴交于A(-2,0),B(6,0)两点.
轴交于A(-2,0),B(6,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)点P为y轴右侧抛物线上一个动点,若S△PAB=32,求出此时P点的坐标.
-
科目: 来源: 题型:
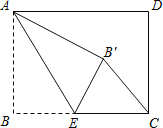
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 .
相关试题

