
【题目】如图,等边△ABC中,AB=6,D是AC的中点,E是BC延长线上的一点,CE=CD,DF⊥BE,垂足为F.
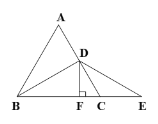
(1)求证:BF=EF;
(2)求△BDE的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)先证△BDE为等腰三角形,依据等腰三角形的性质,即可得到BF=EF;
(2)先求得BE=BC+CE=9,再根据∠DBE=30°,DB=3![]() ,即可得出DF=
,即可得出DF=![]() ,进而得到△BDE的面积.
,进而得到△BDE的面积.
解:(1)∵△ABC为等边三角形,D为AC中点,
∴∠CBD=30°,∠ACB=60°,
又∵CD=CE,
∴∠CDE=∠CED=30°,
∴BD=DE,则△BDE为等腰三角形,
∵DF⊥BE,
∴BF=EF;
(2)∵△ABC为等边三角形,D为AC中点,AB=6,
∴AD=CD,CE=CD,∠DBC=![]() ,
,
∴CE=CD=3,
∴BE=BC+CE=9,
∴![]() ,
,
∴DF=![]() ,
,
S△BDE=![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
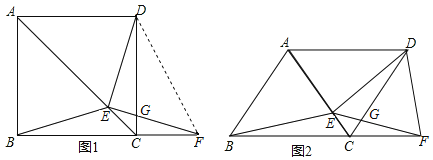
【题目】如图1,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 交
交![]() 于
于![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,求
,求![]() ;
;
(3)如图2,若把正方形![]() 改为菱形
改为菱形![]() ,其他条件不变,当
,其他条件不变,当![]() 时,猜想
时,猜想![]() 与
与![]() 的数量关系,并证明你的猜想.
的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
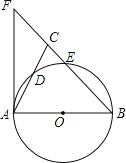
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区![]() 号楼对外销售,已知
号楼对外销售,已知![]() 号楼某单元共
号楼某单元共![]() 层,一楼为商铺,只租不售,二楼以上价格如下:第
层,一楼为商铺,只租不售,二楼以上价格如下:第![]() 层售价为
层售价为![]() 元/米
元/米![]() ,从第
,从第![]() 层起每上升一层,每平方米的售价提高
层起每上升一层,每平方米的售价提高![]() 元,反之每降一层,每平方米的售价降低
元,反之每降一层,每平方米的售价降低![]() 元,已知该单元每套的面积均为
元,已知该单元每套的面积均为![]() 米
米![]()
优惠活动
活动一:若一次性付清所有房款,降价![]() ,另免
,另免![]() 年物业费共
年物业费共![]() 元.
元.
活动二:若购买者一次性付清所有房款,降价![]() ,无赠送.
,无赠送.
(1)请在下表中,补充完整售价![]() (元/米
(元/米![]() )与楼层
)与楼层![]() (
(![]() 取正整数)之间的的数关系式.
取正整数)之间的的数关系式.
楼层 |
|
|
|
|
售价 | 不售 |
|
(2)某客户想购买该单元第![]() 层的一套楼房,若他一次性付清购房款,可以参加如图优惠活动.请你帮助他分析哪种优惠方案更合算
层的一套楼房,若他一次性付清购房款,可以参加如图优惠活动.请你帮助他分析哪种优惠方案更合算

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程序框图的算法思路源于我国古代数学名著《九章算术》,如图所示的程序框图,当输入x的值是17时,根据程序,第一次计算输出的结果是10,第二次计算输出的结果是5,……,这样下去第2019次计算输出的结果是( )
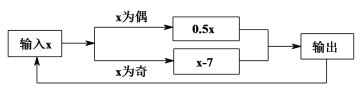
A.-2B.-1C.-8D.-4
查看答案和解析>>
科目:初中数学 来源: 题型:
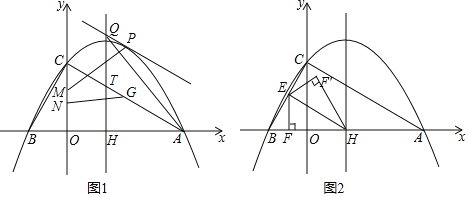
【题目】如图1,抛物线y![]() 2
2![]() 与x轴相交于A、B两点(点A在点B的右侧),与y轴相交于点C,对称轴与x轴相交于点H,与AC相交于点T.
与x轴相交于A、B两点(点A在点B的右侧),与y轴相交于点C,对称轴与x轴相交于点H,与AC相交于点T.
(1)点P是线段AC上方抛物线上一点,过点P作PQ∥AC交抛物线的对称轴于点Q,当△AQH面积最大时,点M、N在y轴上(点M在点N的上方),MN![]() ,点G在直线AC上,求PM+NG
,点G在直线AC上,求PM+NG![]() GA的最小值.
GA的最小值.
(2)点E为BC中点,EF⊥x轴于F,连接EH,将△EFH沿EH翻折得△EF'H,如图所示2,再将△EF'H沿直线BC平移,记平移中的△EF'H为△E'F″H',在平移过程中,直线E'H'与x轴交于点R,则是否存在这样的点R,使得△RF'H'为等腰三角形?若存在,求出R点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
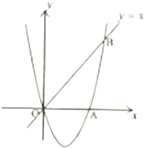
【题目】如图,经过原点![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于另一点
轴交于另一点![]() ,在第一象限内与直线
,在第一象限内与直线![]() 交于点
交于点![]() .
.
(1)求这条抛物线的解析式;
(2)在第四象限内的抛物线上有一点![]() ,满足以
,满足以![]() ,
,![]() ,
,![]() 为顶点的三角形的面积为1,求点
为顶点的三角形的面积为1,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
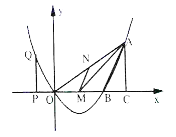
【题目】如图,二次函数的图象经过原点![]() 和
和![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,且对称轴是
,且对称轴是![]() .
.
(1)求二次函数的表达式;
(2)若![]() 是
是![]() 上的一点,作
上的一点,作![]() ,交
,交![]() 于点
于点![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)![]() 是
是![]() 轴上的点,过
轴上的点,过![]() 作
作![]() 轴,与抛物线交于点
轴,与抛物线交于点![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,是否存在点
,是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形与以点
为顶点的三角形与以点![]() 、
、![]() 、
、![]() 为顶点的三角形相似?若存在,求出点
为顶点的三角形相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com