搜索
【题目】如图,圆柱形容器中，高为120cm，底面周长为100cm，在容器内壁离容器底部40cm，的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿40cm与蚊子相对的点A处，
则壁虎捕捉蚊子的最短距离为Cm（容器厚庋忽略不计）.
参考答案：
【答案】130
【解析】解：如图,将容器侧面展开,作A关于EC的对称点A′,连接A′B交EC于F,则A′B即为最短距离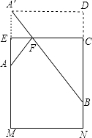 
∵高为120cm，底面周长为100cm，在容器内壁离容器底部40cm的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿40cm与蚊子相对的点A处，
∴A′D=50cm，BD=120cm，
∴在直角△A′DB中,A′B=
=
=130cm .
所以答案是：130 。
【考点精析】利用几何体的展开图和轴对称-最短路线问题对题目进行判断即可得到答案，需要熟知沿多面体的棱将多面体剪开成平面图形，若干个平面图形也可以围成一个多面体；同一个多面体沿不同的棱剪开，得到的平面展开图是不一样的，就是说：同一个立体图形可以有多种不同的展开图；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．
-
科目： 来源： 题型：
查看答案和解析>>【题目】64的立方根是_______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】两个连续偶数的积是288，则这两个数的和是_____________
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（ ）
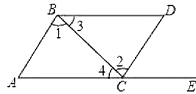
A.∠3=∠A
B.∠l=∠2
C.∠D=∠DCE
D.∠D+∠ACD=180 -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
问题：某饭店工作人员第一次买了13只鸡、5只鸭、9只鹅共用了925元．第二次买了2只鸡、4只鸭、3只鹅共用了320元，试问第三次买了鸡、鸭、鹅各一只共需多少元？(假定三次购买鸡、鸭、鹅的单价不变)
解：设鸡、鸭、鹅的单价分别为x，y，z元．依题意，得
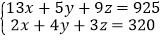
上述方程组可变形为
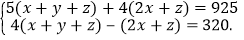
设x＋y＋z＝a，2x＋z＝b，上述方程组可化为：
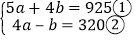
①＋4×②得：a＝____，即x＋y＋z＝____．
答：第三次买鸡、鸭、鹅各一只共需____元．
阅读后，细心的你，可以解决下列问题：(1)上述材料中a＝ ；
(2)选择题：上述材料中的解答过程运用了 思想方法来指导解题．
A．整体 B．数形结合 C．分类讨论
(3)某校体育组购买体育用品甲、乙、丙、丁的件数和用钱金额如下表：
品名
次数
甲
乙
丙
丁
用钱金额(元)
第一次购买件数
5
4
3
1
1 882
第二次购买件数
9
7
5
1
2 764
那么购买每种体育用品各一件共需多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】 正方形
的边长为1，点
是
边上的一个动点（与
不重合)，以
为顶点在所在直线的上方作
. (1)当
经过点
时，①请直接填空：
（可能，不可能）过
点；（图1仅供分析）②如图2,在
上截取
，过
点作
垂直于直线
,垂足为点
，册
于
，求证：四边形
为正方形.（2）当
不过点
时，设交边
于
,且
.在
上存在点
,过
点作
垂直于直线
,垂足为点
，使得
，连接
，求四边形
的最大面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市总预算
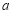亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始，市政府在每年年初分别对三项工程进行不同数额的投资.2015年年初，对线路敷设、搬迁安置的投资分别是辅助配套投资的2倍、4倍.随后两年，线路敷设投资每年都增加
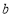亿元，预计线路敷设三年总投资为54亿元时会顺利如期完工；搬迁安置投资从2016年初开始遂年按同一百分数递减，依此规律，在 2017年年初只需投资5亿元，即可顺利如期完工；辅助配套工程在2016年年初的投资在前一年基础上的增长率是线路敷设2016年投资增长率的1.5倍，2017年年初的投资比该项工程前两年投资的总和还多4亿元，若这样，辅助配套工程也可以如期完工.经测算，这三年的线路敷设、辅助配套工程的总投资资金之比达到3: 2. （1）这三年用于辅助配套的投资将达到多少亿元？
（2）市政府2015年年初对三项工程的总投资是多少亿元？
（3）求搬迁安置投资逐年递减的百分数.
相关试题
