【题目】如图,已知抛物线y=x2+bx+c交x轴于点A(﹣1,0)、B(2,0),交y轴于点C,抛物线的对称轴交x轴于点H,直线y=kx(k>0)交抛物线于点M、N(点M在N的右侧),交抛物线的对称轴于点D.
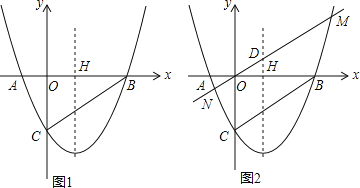
(1)求b和c的值;
(2)如图(1),若将抛物线y=x2+bx+c沿y轴方向向上平移![]() 个单位,求证:所得新抛物线图象均在直线BC的上方;
个单位,求证:所得新抛物线图象均在直线BC的上方;
(3)如图(2),若MN∥BC.
①连接CD、BM,判断四边形CDMB是否为平行四边形,说明理由;
②以点D为圆心,DH长为半径画圆⊙D,点P、Q分别为抛物线和⊙D上的点,试求线段PQ长的最小值.
参考答案:
【答案】(1)b=﹣1,c=﹣2;(2)证明见解析;(3)①不是平行四边形,理由见解析②![]()
【解析】
试题分析:(1)把A、B两点代入转化为方程组,即可解决问题.
(2)由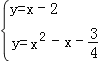 消去y得到x2﹣2x+
消去y得到x2﹣2x+![]() =0用判别式解决.
=0用判别式解决.
(3)根据两点间距离公式,利用配方法转化为二次函数最值问题即可解决.
解:(1)由题意![]() ,
,
解得![]() ,
,
所以b=﹣1,c=﹣2.
(2)∵抛物线为y=(x+1)(x﹣2)=x2﹣x﹣2,沿y轴方向向上平移![]() 个单位,
个单位,
∴新抛物线为y=x2﹣x﹣![]() ,
,
设直线BC为y=kx+b,由题意得![]() ,
,
解得![]() ,
,
所以直线BC为y=x﹣2,
由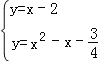 消去y得到x2﹣2x+
消去y得到x2﹣2x+![]() =0,
=0,
∵△=4﹣5=﹣1<0,
∴方程组无解,抛物线与直线BC没有交点.
(3)①∵MN∥BC,
∴k=1,OM>OB,
∴MN≠BC,
∴四边形CDMB不是平行四边形.
②设点P(m,m2﹣m﹣2),
∵点D坐标为(![]() ,
,![]() ),
),
∴PD2=(m﹣![]() )2+(m2﹣m﹣
)2+(m2﹣m﹣![]() )2
)2
=(m﹣![]() )2+[(m﹣
)2+[(m﹣![]() )2﹣
)2﹣![]() ]2
]2
=(m﹣![]() )4﹣
)4﹣![]() (m﹣
(m﹣![]() )2+
)2+![]()
=[(m﹣![]() )2﹣
)2﹣![]() ]2+
]2+![]() ,
,
∴PD2的最小值=![]() ,
,
∴PD的最小值=![]() ,
,
∵DQ=![]() ,
,
∴线段PQ的最小值=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两种水稻试验田连续5年的平均单位面积产量如下:(单位:吨/公顷)
品种
第1年
第2年
第3年
第4年
第5 年
甲
9.8
9.9
10.1
10
10.2
乙
9.4
10.3
10.8
9.7
9.8
(1)哪种水稻的平均单位面积产量比较高?
(2)哪种水稻的产量比较稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分类
﹣3,0.45,
 ,0,9,﹣1,﹣1
,0,9,﹣1,﹣1 ,10,﹣3.14
,10,﹣3.14(1)正整数:{ …}
(2)负整数:{ …}
(3)整数:{ …}
(4)分数:{ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学学习计算机打字,甲打一篇3000字的文章与乙打一篇2400字的文章所用的时间相同.已知甲每分钟比乙每分钟多打12个字,问甲、乙两人每分钟各打多少个字?
李明同学是这样解答的:
设甲同学打印一篇3 000字的文章需要x分钟,
根据题意,得
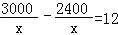 (1)
(1)解得:x=50.
经检验x=50是原方程的解.(2)
答:甲同学每分钟打字50个,乙同学每分钟打字38个.(3)
(1)请从(1)、(2)、(3)三个步骤说明李明同学的解答过程是否正确,若有不正确的步骤改正过来.
(2)请你用直接设未知数列方程的方法解决这个问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我区某一周的最高气温统计如下表:
最高气温(℃)
13
15
17
18
天 数
1
1
2
3
则这组数据的中位数与众数分别是( )
A. 17,17 B. 17,18 C. 18,17 D. 18,18
-
科目: 来源: 题型:
查看答案和解析>>【题目】10位学生分别购买如下尺码的鞋子:20,20,21,22,22,22,22,23,23,24(单位:cm).这组数据的平均数、中位数、众数三个指标中鞋店老板最喜欢的是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ab2﹣4ab+4a=_________.
相关试题

