【题目】如图,矩形ABCD中,AB=6,BC=4.
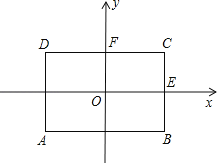
(1)画出以矩形的两条对称轴为坐标轴(x轴平行于AB)的平面直角坐标系,并写出点A,BC的中点E,DC的中点F的坐标;
(2)求过点A,E,F三点的抛物线的解析式,并写出此抛物线的顶点坐标.
参考答案:
【答案】(1)A(﹣3,﹣2),E(3,0),F(0,2).
(2)抛物线y=﹣![]() x2+
x2+![]() x+2,顶点(
x+2,顶点(![]() ).
).
【解析】
试题分析:(1)根据矩形的对称性可知:E、F分别在x轴和y轴上,因此E(3,0),F(0,2);由于DF=![]() CD=3,BE=
CD=3,BE=![]() BC=2,因此A(﹣3,﹣2).
BC=2,因此A(﹣3,﹣2).
(2)可根据(1)题得出的A、E、F三点坐标,用待定系数法可求出抛物线的解析式.进而可用配方法或公式法求出抛物线顶点坐标.
解:(1)A(﹣3,﹣2),E(3,0),F(0,2).
(2)易知:A(﹣3,﹣2).
设抛物线的解析式为y=ax2+bx+c,由于抛物线过A、E、F三点,则有:
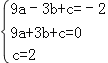 ,
,
解得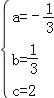 ,
,
∴抛物线y=﹣![]() x2+
x2+![]() x+2,顶点(
x+2,顶点(![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:x2y﹣(xy﹣x2y)﹣2(﹣xy+x2y)﹣5,其中x=﹣1,y=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一盒圆珠笔有12支,售价24元,用y(元)表示圆珠笔的售价,x表示圆珠笔的支数,那么y与x之间的关系应该是_____.
-
科目: 来源: 题型:
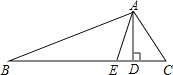
查看答案和解析>>【题目】已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=40°,∠C=60°.求∠DAE的度数.
-
科目: 来源: 题型:
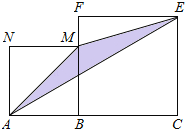
查看答案和解析>>【题目】如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为
S3;则S3﹣S2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们可以用几何图形来解决一些代数问题,如图(甲)可以来解释(a+b)2=a2+2ab+b2,
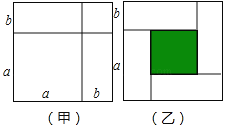
(1)图(乙)是四张全等的矩形纸片拼成的图形,请利用图中阴影部分面积的不同表示方法,写出一个关于a,b代数恒等式表示 ;
(2)请构图解释:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(3)请通过构图因式分解:a2+3ab+2b2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处, BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2015与A间的距离为( )

A.3 B.4 C.5 D.6
相关试题

