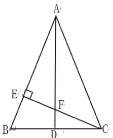
【题目】如图,AD为△ABC的中线,AB=AC,∠BAC=45.过点C 作CE⊥AB,垂足为E,CE与AD交于点F.
(1)求证: △AEF≌△CEB;
(2)试探索AF与CD的数量关系,并说明理由.
参考答案:
【答案】(1) 见解析;(2) ![]() ,理由见解析
,理由见解析
【解析】
(1)根据三线合一可得:![]() ,AD⊥BC,从而得出∠ADB=90°,然后根据等腰直角三角形的判定,可得△AEC为等腰直角三角形,从而得出AE=CE,再根据同角的余角相等可得∠BAD =∠ECB,最后利用ASA即可证出△AEF≌△CEB;
,AD⊥BC,从而得出∠ADB=90°,然后根据等腰直角三角形的判定,可得△AEC为等腰直角三角形,从而得出AE=CE,再根据同角的余角相等可得∠BAD =∠ECB,最后利用ASA即可证出△AEF≌△CEB;
(2)根据全等三角形的性质可得:AF=CB,从而得出![]() .
.
解:(1)∵AD为△ABC的中线,AB=AC,
∴![]() ,AD⊥BC,
,AD⊥BC,
∴∠ADB=90°
∴∠BAD+∠B=90°
∵CE⊥AB,∠BAC=45
∴∠BEC=∠FEA=90°,△AEC为等腰直角三角形
∴∠ECB+∠B=90°,AE=CE
∴∠BAD =∠ECB
在△AEF和△CEB中
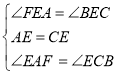
∴△AEF≌△CEB;
(2)![]() ,理由如下:
,理由如下:
∵△AEF≌△CEB
∴AF=CB
∵![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
-
科目: 来源: 题型:
查看答案和解析>>【题目】飞镖随机地掷在下面的靶子上.
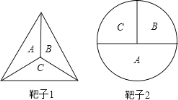
 在每一个靶子中,飞镖投到区域
在每一个靶子中,飞镖投到区域 、
、 、
、 的概率是多少?
的概率是多少? 在靶子
在靶子 中,飞镖投在区域
中,飞镖投在区域 或
或 中的概率是多少?
中的概率是多少? 在靶子
在靶子 中,飞镖没有投在区域
中,飞镖没有投在区域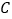 中的概率是多少?
中的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
①AM=AD+MC;②AM=DE+BM;③DE2=ADCM;④点N为△ABM的外心.其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
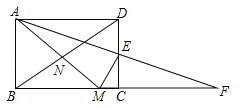
查看答案和解析>>【题目】下面是课本中“作一个角等于已知角”的尺规作图过程.已知:∠AOB. 求作:一个角,使它等于∠AOB.作法:如图
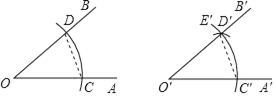
(1)作射线O'A';
(2)以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
(3)以O'为圆心,OC为半径作弧C'E',交O'A'于C';
(4)以C'为圆心,CD为半径作弧,交弧C'E'于D';
(5)过点D'作射线O'B'.
则∠A'O'B'就是所求作的角.
请回答:该作图的依据是( )
A.SSSB.SASC.ASAD.AAS
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,求∠AEB的度数.
相关试题

