【题目】随着人们生活水平的提高,对饮水品质的需求也越来越高,某商场购进甲、乙两种型号的净水器,每台甲型净水器比每台乙型净水器进价多200元,已知用5万元购进甲型净水器与用4.5万元购进乙型净水器的数量相等.
(1)求每台甲型,乙型净水器的进价各是多少元?
(2)该商场计划花费不超过9.8万元购进两种型号的净水器共50台进行销售,甲型净水器每台销售2500元,乙型净水器每台售价2200元,商场还将从销售甲型净水器的利润中按每台a元(70<a<80)捐献给贫困地区作为饮水改造扶贫资金.设该公司售完50台净水器并捐献扶贫资金后获得的利润为W元,求W的最大值.
参考答案:
【答案】(1)甲型净水器的进价为2000元/台,乙型净水器的进价为1800元/台;(2)W的最大值为24000-40a.
【解析】
(1)设乙型净水器的进价为x元/台,则甲型净水器的进价为(x+200)元/台,根据用5万元购进甲型净水器与用4.5万元购进乙型净水器的数量相等列方程可求出x的值,检验后再求出x+200的值即可得答案;
(2)设购进甲型净水器x台,则购进乙型净水器为(50-x)台,根据总花费不超过9.8万元可求出x的取值范围;根据利润W=(甲售价-进价-a)x+(乙售价-乙进价)(50-x),利用一次函数的性质及增减性即可得答案.
(1)设乙型净水器的进价为x元/台,则甲型净水器的进价为(x+200)元/台,
∵用5万元购进甲型净水器与用4.5万元购进乙型净水器的数量相等,
∴![]() ,
,
解得:x=1800,
经检验:x=1800是原分式方程的解,
∴x+200=2000,
答:甲型净水器的进价为2000元/台,乙型净水器的进价为1800元/台.
(2)设购进甲型净水器x台,则购进乙型净水器为(50-x)台,
∵计划花费不超过9.8万元购进两种型号的净水器共50台进行销售,
∴2000x+1800(50-x)≤98000,
解得:x≤40,
∵x为整数,
∴0≤x≤40,
∵该公司售完50台净水器并捐献扶贫资金后获得的利润为W元,
∴W=(2500-2000-a)x+(2200-1800)(50-x)=(100-a)x+20000,
∵70<a<80,
∴100-a>0,
∴W随x的增大而增大,
∴当x=40时,W有最大值24000-40a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:善于思考的小明在解方程组
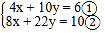 时,采用了一种“整体代换”的解法,解法如下:
时,采用了一种“整体代换”的解法,解法如下:解:将方程②8x+20y+2y=10,变形为 2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则 y=﹣1;把 y=﹣1 代入①得,x=4,所以方程组的解为:
 请你解决以下问题:
请你解决以下问题:(1)试用小明的“整体代换”的方法解方程组

(2)已知 x、y、z,满足
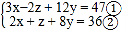 试求 z 的值.
试求 z 的值. -
科目: 来源: 题型:
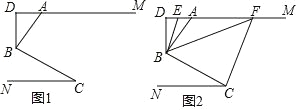
查看答案和解析>>【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为提倡节约用水,准备实行自来水阶梯计算方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为了更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是___________
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区10万用户中约有多少用户的用水全部享受基本价格?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
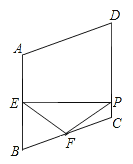
A. 35° B. 45° C. 50° D. 55°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
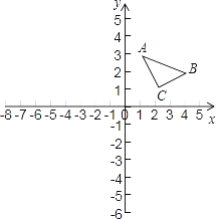
(1)作出与△ABC关于x轴对称的△A1B1C1, 并写出A1、B1、C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2, 使
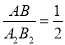 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.易证:CE=CF.

(1)在图1中,若G在AD上,且∠GCE=45°.试猜想GE,BE,GD三线段之间的数量关系,并证明你的结论.
(2)运用(1)中解答所积累的经验和知识,完成下面两题:
①如图2,在四边形ABCD中∠B=∠D=90°,BC=CD,点E,点G分别是AB边,AD边上的动点.若∠BCD=α,∠ECG=β,试探索当α和β满足什么关系时,图1中GE,BE,GD三线段之间的关系仍然成立,并说明理由.
②在平面直角坐标中,边长为1的正方形OABC的两顶点A,C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图3).设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?若不变,请直接写出结论.
相关试题

