【题目】(10分)如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系,并从所得的四个关系中任选一个加以说明,证明所探究的结论的正确性。
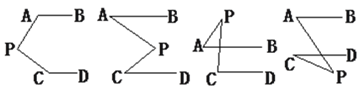
结论⑴____________________⑵___________________
⑶__________________⑷___________________
选择结论____,说明理由是什么。
参考答案:
【答案】 ∠APC+∠PAB+∠PCD=360° ∠APC=∠PAB+∠PCD ∠APC=∠PCD-∠PAB ∠APC=∠PAB-∠PCD (2)理由见解析
【解析】理由如下:
过P点作PQ∥AB
∵AB∥CD,PQ∥AB
∴PQ∥CD
∴∠QPC=∠C
∵PQ∥AB
∴∠QPA=∠A,
∵∠APC=∠APQ+∠QPC
∴∠APC=∠A+∠C
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列4个命题:①矩形的对角线互相平分且相等;②对角线互相垂直的四边形是菱形;
③正方形的两条对角线相等;④等腰三角形底边上的中点到两腰的距离相等.其中正确的是( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
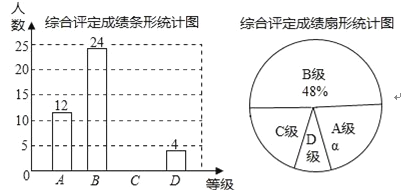
(1)在这次调查中,一共抽取了 名学生,α= %;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为 度;
(4)若该校共有2000名学生,请你估计该校D级学生有多少名?
-
科目: 来源: 题型:
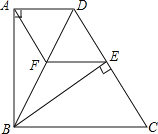
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】P1(x1,y1),P2(x2,y2)是一次函数y=-2x+5图像上的两点,且x1<x2,则y1与y2的大小关系是( )
A.y1<y2B.y1=y2C.y1>y2D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A( 1-a, 5 ),B( 3 , b )关于y轴对称,则a+b= 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=ax-6与抛物线y=x2-4x+3只有一个交点,则a的值是____.
相关试题

