【题目】阅读下面材料:
材料一:分解因式是将一个多项式化为若干个整式积的形式的变形,“十字相乘法”可把某些二次三项式分解为两个一次式的乘积,具体做法如下:对关于![]() ,
,![]() 的二次三项式
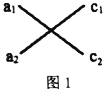
的二次三项式![]() ,如图1,将
,如图1,将![]() 项系数
项系数![]() ,作为第一列,
,作为第一列,![]() 项系数
项系数![]() ,作为第二列,若
,作为第二列,若![]() 恰好等于
恰好等于![]() 项的系数
项的系数![]() ,那么
,那么![]() 可直接分解因式为:
可直接分解因式为:![]()
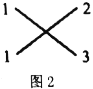
示例1:分解因式:![]()
解:如图2,其中![]() ,
,![]() ,而
,而![]() ;
;
∴![]() ;
;
示例2:分解因式:![]() .
.
解:如图3,其中![]() ,
,![]() ,而
,而![]() ;
;
∴![]() ;
;

材料二:关于![]() ,
,![]() 的二次多项式
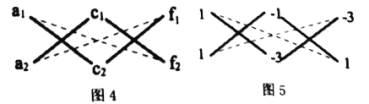
的二次多项式![]() 也可以用“十字相乘法”分解为两个一次式的乘积.如图4,将
也可以用“十字相乘法”分解为两个一次式的乘积.如图4,将![]() 作为一列,
作为一列,![]() 作为第二列,
作为第二列,![]() 作为第三列,若
作为第三列,若![]() ,
,![]() ,
,![]() ,即第1、2列,第1、3列和第2、3列都满足十字相乘规则,则原式分解因式的结果为:
,即第1、2列,第1、3列和第2、3列都满足十字相乘规则,则原式分解因式的结果为:![]() ;
;
示例3:分解因式:![]() .
.
解:如图5,其中![]() ,
,![]() ,
,![]() ;
;
满足![]() ,
,![]() ;
;
∴![]()
请根据上述材料,完成下列问题:
(1)分解因式:![]() ;
;![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 均为整数,且关于
均为整数,且关于![]() ,
,![]() 的二次多项式
的二次多项式![]() 可用“十字相乘法”分解为两个一次式的乘积,求出
可用“十字相乘法”分解为两个一次式的乘积,求出![]() 的值,并求出关于
的值,并求出关于![]() ,
,![]() 的方程
的方程![]() 的整数解.
的整数解.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() 和
和![]()
【解析】
(1)①直接用十字相乘法分解因式;②把某个字母看成常数用十字相乘法分解即可;
(2)用十字相乘法把能分解的集中情况全部列出求出m值.
解:(1)①1=1×1,2=1×2,3=1×1+1×2,
∴原式=![]() ;
;
②1=1×1,6=(-2)×(-3),-20=5×(-4)
满足(-5)=1×(-2)+1×(-3),1=1×5+1×(-4),2=(-2)×5+(-3)×(-4)
∴原式=![]() ;
;
(2)①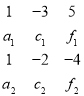
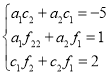
②![]()
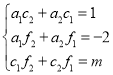
![]()
![]()
∴![]()
![]()
∴![]()
当![]() 时,
时,![]()
![]() 或
或![]() ,
,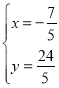 (舍),
(舍),![]()
当![]() 时,
时,![]()
![]() 或
或![]() ,
,![]() 或
或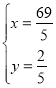 (舍)
(舍)
综上所述,方程![]() 的整数解有
的整数解有![]() 和
和![]() ;
;
方法二:![]()
![]()
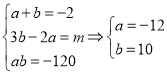 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

-
科目: 来源: 题型:
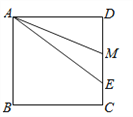
查看答案和解析>>【题目】如图所示,在正方形
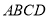 中,
中, 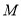 是
是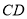 的中点,
的中点, 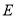 是
是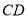 上一点,且
上一点,且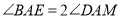 .求证:
.求证: 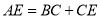 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抖音将“重庆洪崖洞”抖成了全国知名景点,五一期间,很多外地游客都慕名前来打卡.小丽和小萌二人约定分别从贵阳和遵义自驾到重庆游玩,由于贵阳到重庆的路程更远,所以小丽先出发,2.2小时后小萌才出发追赶小丽,她们二人离贵阳的距离
 (千米)与小丽行驶的时间
(千米)与小丽行驶的时间 (小时)之间的关系图像如图所示,请根据图像回答下列问题:
(小时)之间的关系图像如图所示,请根据图像回答下列问题:(1)小丽的速度为 千米/小时,小萌的速度为 千米/小时;
(2)当小萌追上小丽时,她们离贵阳的距离是多少千米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】“2017年张学友演唱会”于6月3日在我市观山湖奥体中心举办,小张去离家2520米的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有23分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小张骑车的时间比跑步的时间少用了4分钟,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度;
(2)如果小张在家取票和寻找“共享单车”共用了5分钟,他能否在演唱会开始前赶到奥体中心?说明理由. -
科目: 来源: 题型:
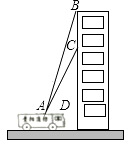
查看答案和解析>>【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
-
科目: 来源: 题型:
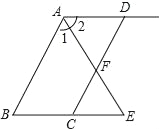
查看答案和解析>>【题目】如图,已知AD∥BC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AB∥DC,把下面的说理过程补充完整.
证明:∵AD∥BC(已知)
∴∠2=∠E(___________________________)
∵AE平分∠BAD(已知)
∴∠1=∠2 (_________________________)
∴∠1=∠E(___________________________)
∵∠CFE=∠E(已知)
∴∠1=∠______(______________________)
∴AB∥CD(_________________________________)
相关试题

