【题目】学校餐厅中,一张桌子可坐6人,现有以下两种摆放方式:
(1)当有5张桌子时,第一种方式能坐 人,第二种方式能坐 人.
(2)当有n张桌子时,第一种方式能坐 人,第二种方式能坐 人.
(3)新学期有200人在学校就餐,但餐厅只有60张这样的餐桌,若你是老师,你打算选择以下哪种方式来摆放餐桌?为什么?

参考答案:
【答案】(1)22,14; ( 2)(2+4n), (4+2n); (3)解: 打算以第一种方式来摆放餐桌,见解析
【解析】
(1)第一种中,只有一张桌子是6人,后边多一张桌子多4人,即有n张桌子时是6+4(n-1)=4n+2;第二种中,有一张桌子时6人,后边多一张桌子多2人,即6+2(n-1)=2n+4,将n=5代入即可得出答案;
(2)根据(1)找出的规律即可得出答案;
(3)分别求出n=60时,两种不同的摆放方式对应的人数,即可得出答案.
解:(1)第一种22人,第二种14人;
(2)第一种(2+4n)人,第二种(4+2n)人;
(3)打算以第一种方式来摆放餐桌
∵第一种中,当n=60时,4×60+2=242>200
第二种中,当n=60时,2×60+4=124<200
∴选择第一种摆放方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有三个点A、B、C,表示的数分别是﹣4、﹣2、3,请回答:

(1)若使C、B两点的距离与A、B两点的距离相等,则需将点C向左移动 个单位;
(2)若移动A、B、C三点中的两个点,使三个点表示的数相同,移动方法有 种,其中移动所走的距离和最小的是 个单位;
(3)若在原点处有一只小青蛙,一步跳1个单位长.小青蛙第1次先向左跳1步,第2次再向右跳3步,然后第3次再向左跳5步,第4次再向右跳7步,…,按此规律继续跳下去,那么跳第100次时,应跳 步,落脚点表示的数是 ;
(4)若有两只小青蛙A、B,它们在数轴上的点表示的数分别为整数x、y,且|x﹣2|+|y+3|=2,求两只小青蛙A、B之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算与化简
(1)-18+21+(-13)
(2)-81÷
 ×
×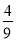 ÷(-16)
÷(-16)(3)(
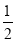 +
+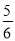 -
-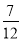 )×(-24)
)×(-24)(4)-22-
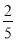 ×[4-(-3)2]
×[4-(-3)2](5)化简:5(3x2y-xy2)-4(-xy2+2x2y)
(6)先化简,再求值:-
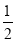 x+2(x-
x+2(x-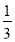 y2) - (-
y2) - (-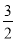 x+
x+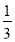 y2);其中x=2,y=
y2);其中x=2,y=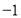 .
. -
科目: 来源: 题型:
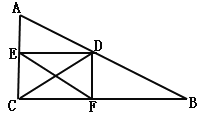
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=4,点D为边AB上一动点,DE⊥AC,DF⊥BC,垂足为E,F. 连接EF,CD.
(1)求证:EF=CD;
(2)当EF为何值时,EF∥AB;
(3)当四边形ECFD为正方形时,求EF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:

(1)这8筐白菜中,最接近25千克的那筐白菜为______千克;
(2)以每筐25千克为标准,这8筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这8筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2015湖州)如图,已知抛物线C1:
 和C2:
和C2: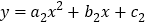 都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是____________________和__________________.
都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是____________________和__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成ABABC共5个区,A区是边长为a m的正方形,C区是4个边长为b m的小正方形组成的正方形.
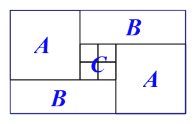
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40 m,b=20 m,求整个长方形运动场的面积.
相关试题

