Question

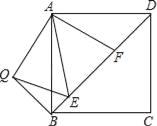
【题目】如图，在正方形ABCD中，E、F是对角线BD上两点，且∠EAF=45°，将△ADF绕点A顺时针旋转90°后，得到△ABQ，连接EQ，求证：

（1）EA是∠QED的平分线；

（2）EF2=BE2+DF2．

Answer 1

【答案】详见解析.

【解析】试题分析：(1)、直接利用旋转的性质得出△AQE≌△AFE（SAS），进而得出∠AEQ=∠AEF，即可得出答案；(2)、利用（1）中所求，再结合勾股定理得出答案．

试题解析：(1)、∵将△ADF绕点A顺时针旋转90°后，得到△ABQ， ∴QB=DF，AQ=AF，∠ABQ=∠ADF=45°，

∴△AQE≌△AFE（SAS）， ∴∠AEQ=∠AEF， ∴EA是∠QED的平分线；

(2)、由（1）得△AQE≌△AFE， ∴QE=EF， 在Rt△QBE中，

QB2+BE2=QE2， 则EF2=BE2+DF2．