【题目】阅读题.
材料一:若一个整数m能表示成a2-b2(a,b为整数)的形式,则称这个数为“完美数”.例如,3=22-12,9=32-02,12=42-22,则3,9,12都是“完美数”;再如,M=x2+2xy=(x+y)2-y2,(x,y是整数),所以M也是”完美数”.
材料二:任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q).如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并且规定F(n)=![]() .例如18=1×18=2×9=3×6,这三种分解中3和6的差的绝对值最小,所以就有F(18)=
.例如18=1×18=2×9=3×6,这三种分解中3和6的差的绝对值最小,所以就有F(18)=![]() .请解答下列问题:
.请解答下列问题:
(1)8______(填写“是”或“不是”)一个完美数,F(8)= ______.
(2)如果m和n都是”完美数”,试说明mn也是完美数”.
(3)若一个两位数n的十位数和个位数分别为x,y(1≤x≤9),n为“完美数”且x+y能够被8整除,求F(n)的最大值.
参考答案:
【答案】(1)是,![]() ;(2)说明见解析; (3)
;(2)说明见解析; (3)![]() .
.
【解析】
(1)利用“完美数”的定义可得;
(2)根据完全平方公式,可证明mn是“完美数”;
(3)两个一位数相加能被8整除,说明x+y=8或16, 这样可得正整数n为79,97,88,71,17,26,62,35,53,44共10种, 根据n为“完美数”可把n=26和n=62舍去,再根据n的最佳分解确定出F(n)的最大值.
(1) )∵8=32-12
∴8是完美数,
F(8)=![]() =
=![]()
故答案为:是, ![]() .
.
(2)设m=![]() , n=
, n=![]() ,其中a,b,c,d均为整数,
,其中a,b,c,d均为整数,
则mn= (![]() )(
)(![]() )
)
=![]()
=![]()
∵a,b,c,d均为整数
∴ac+bd与ad+bc也是整数,即mn是“完美数”.
(3) ∵两个一位数相加能被8整除,
∴ x+y=8或16,
∴n=79或97或88或71或17或26或62或35或53或44,
∵n为“完美数”,
∴n=79或97或88或71或17或35或53或44,
其中F(79)=![]() ,F(97)=
,F(97)= ![]() ,F(88)=
,F(88)=![]() , F(71)=
, F(71)=![]() , F(17)=
, F(17)=![]() , F(35)=
, F(35)=![]() , F(53)=
, F(53)=![]() , F(44)=
, F(44)=![]() ,
,
∴F(n)的最大值为![]() .
.
-
科目: 来源: 题型:
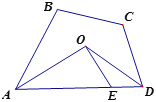
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=104°,∠C=120°,AO、DO分别平分∠BAD和∠CDA,EO⊥AO,则∠EOD=________
-
科目: 来源: 题型:
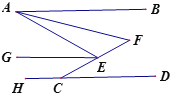
查看答案和解析>>【题目】如图,已知AB∥HD,EG平分∠AEC,EG∥AB,AF平分∠BAE,CE的延长线交AF于点F,若∠HCE=
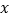 °,∠F=
°,∠F=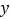 °,用含
°,用含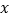 的代数式表示
的代数式表示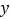 ,则
,则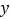 =_______
=_______
-
科目: 来源: 题型:
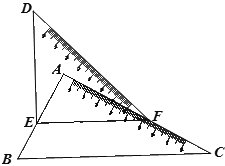
查看答案和解析>>【题目】有一副直角三角板按如图所示放置,点E、F分别在线段AB和线段AC上,∠DEF=∠BAC=90°,∠D=45°,∠C=30°.
(1)若∠DEA=28°,求∠DFA的度数.
(2)当∠DFC等于多少度时,EF∥BC?说说你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.
(1)此时梯子顶端离地面多少米?
(2)若梯子顶端下滑4米,那么梯子底端将向左滑动多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求A,B两点的坐标;
(2)过B点作直线与x轴交于点P,若△ABP的面积为
 ,试求点P的坐标.
,试求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:对于形如
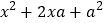 这样的二次三项式,可以用公式法将它分解成
这样的二次三项式,可以用公式法将它分解成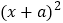 的形式.但对于二次三项式
的形式.但对于二次三项式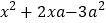 ,就不能直接运用公式了.此时,我们可以在二次三项式
,就不能直接运用公式了.此时,我们可以在二次三项式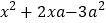 中先加上一项
中先加上一项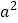 ,使它与
,使它与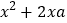 的和成为一个完全平方式,再减去
的和成为一个完全平方式,再减去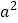 ,整个式子的值不变,于是有:
,整个式子的值不变,于是有: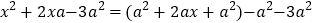
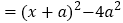
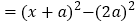
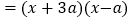
像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”,利用“配方法",解决下列问题:
(1)分解因式:
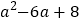 .
.(2)比较代数式
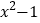 与
与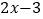 的大小.
的大小.
相关试题

