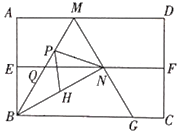
【题目】如图,四边形是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:①∠ABN= 60°;②AM=1;③![]() ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是
;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是![]() .其中正确结论的序号是___________.
.其中正确结论的序号是___________.
参考答案:
【答案】①④⑤
【解析】如图1,连接AN,
∵EF垂直平分AB,
∴AN=BN,
根据折叠的性质,可得
AB=BN,
∴AN=AB=BN.
∴△ABN为等边三角形。
∴∠ABN=60°,∠PBN=60°÷2=30°,
即结论①正确;
∵∠ABN=60°,∠ABM=∠NBM,
∴∠ABM=∠NBM=60°÷2=30°,
∴AM=ABtan30°=2×![]() =
=![]() ,
,
即结论②不正确。
∵EF∥BC,QN是△MBG的中位线,
∴QN=![]() BG;
BG;
∵BG=BM=AB÷cos∠ABM=2÷![]() =
=![]() ,
,
∴QN=![]() ×
×![]() =
=![]() ,
,
即结论③不正确。
∵∠ABM=∠MBN=30°,∠BNM=∠BAM=90°,
∴∠BMG=∠BNM∠MBN=90°30°=60°,
∴∠MBG=∠ABG∠ABM=90°30°=60°,
∴∠BGM=180°60°-60°=60°,
∴∠MBG=∠BMG=∠BGM=60°,
∴△BMG为等边三角形,
即结论④正确。
∵△BMG是等边三角形,点N是MG的中点,
∴BN⊥MG,∴BN=BGsin60°=![]() ×
×![]() =2,
=2,
根据条件易知E点和H点关于BM对称,
∴PH=PE,
∴P与Q重合时,PN+PH的值最小,此时PN+PH=PN+PE=EN,
∵EN=![]() =
=![]() ,
,
∴PN+PH=![]() ,
,
∴PN+PH的最小值是![]() ,
,
即结论⑤正确。
故答案为:①④⑤。
-
科目: 来源: 题型:
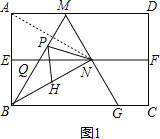
查看答案和解析>>【题目】取一张矩形纸片进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图1;第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B',得Rt△AB'E,如图2;第三步:沿EB'线折叠得折痕EF,使A点落在EC的延长线上,如图3.
利用展开图4探究:
(1)△AEF是什么三角形?证明你的结论;
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
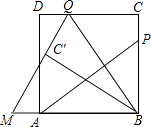
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4.点P以每秒一个单位长度的速度沿着B-C-A运动,
 始终与AB相切,设点P运动的时间为t,0P的面积为y.则y与t之间的函效关系图像大致是( )
始终与AB相切,设点P运动的时间为t,0P的面积为y.则y与t之间的函效关系图像大致是( )
A.
 B.
B. 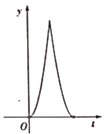 C.
C. 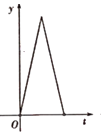 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)(15x2y﹣10xy2)÷(﹣5xy); (2)(m+2n+3)(m+2n﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二元一次方程2x+y=11的非负整数解有____________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
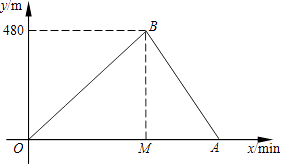
(1)A点所表示的实际意义是;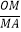 =;
=;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
相关试题

