搜索
【题目】甲、乙、丙三名射击运动员在某场测试中各射击10次，3人的测试成绩如下表
则甲、乙、丙3名运动员测试成绩最稳定的是 （ ）
A．甲 B．乙 C．丙 D．3人成绩稳定情况相同
参考答案：
【答案】C
【解析】
试题分析：根据表中数据计算可得三人的平均成绩均为8.5，所以甲的方差为
=[（7-8.5）2×2+（8-8.5）2×3+（9-8.5）2×3+（10-8.5）2×2]÷10=2，乙的方差为
=[（7-8.5）2+（8-8.5）2×4+（9-8.5）2×4+（10-8.5）2]÷10=0.65，丙的方差为
=[（8-8.5）2×5+（9-8.5）2×5]÷10=0.25，所以0.25＜0.65＜2.所以甲、乙、丙3名运动员测试成绩最稳定的是丙．故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】首条贯通丝绸之路经济带的高铁线﹣宝兰客专进入全线拉通试验阶段，宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义．试运行期间，一列动车从西安开往西宁，一列普通列车从西宁开往西安，两车同时出发，设普通列车行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示y与x之间的函数关系，根据图象进行一下探究：
【信息读取】
（1）西宁到西安两地相距 千米，两车出发后 小时相遇；
（2）普通列车到达终点共需 小时，普通列车的速度是 千米/小时．
【解决问题】
（3）求动车的速度；
（4）普通列车行驶t小时后，动车到达终点西宁，求此时普通列车还需行驶多少千米到达西安？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下：
对这两名运动员的成绩进行比较，下列四个结论中，不正确的是（ ）
A. 甲运动员得分的极差大于乙运动员得分的极差
B. 甲运动员得分的中位数大于乙运动员得分的中位数
C. 甲运动员得分的平均数大于乙运动员得分的平均数
D. 甲运动员的成绩比乙运动员的成绩稳定
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知EC∥AB，∠EDA=∠ABF．
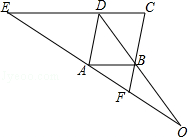
（1）求证：四边形ABCD是平行四边形；
（2）求证：OA2=OEOF． -
科目： 来源： 题型：
查看答案和解析>>【题目】神奇的数学世界是不是只有锻炼思维的数字游戏？每天都在面对繁杂的数字计算？答案当然是否定的，曼妙的数学畅游在迷人的数字和丰富多彩的图形之间，将数与形巧妙地融汇在一起，不可分割.我们都知道，实数与数轴上的点一一对应，数轴上的线段可以由端点所对应的实数确定，这是一维的数与形；增加到两条数轴，可以形成平面直角坐标系，这样有序数对与平面内的点一一对应，平面内的多边形及其内容可以由多边形的边上所有点的坐标所确定，这是二维的数与形.而在平面直角坐标系中的图形更是神秘，在平面内任意画一条（或多条）曲线（或直线），它（们）把平面分割成的部分都称为区域，特别地，如果曲线首尾相接，那么形成的有限部分也称为封闭区域.如何研究这些区域呢？当然离不开数，我们可以通过区域内点的坐标规律来刻画图形.反过来，我们也可以根据点坐标的规律在平面直角坐标系内找到它们，画出相应的图形.聪明的你看懂了吗？试着做做看.
（1）分别解不等式
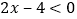和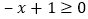
，并把不等式的解集画在同一个数轴上；（2）点P（x,y）在平面直角坐标系的第一象限，并且横坐标与纵坐标分别满足不等式
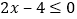和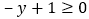
，请画出满足条件的点P所在的最大区域，并求出区域的面积；（3）去掉（2）中“点P在第一象限”这个条件，其余条件保持不变，求满足条件的点P所在最大区域与平面直角坐标系第二、四象限角平分线所围成封闭区域的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算下列各题：（用简便方法计算）
（1）-102n×100×（-10）2n-1； （2）[（-a）（-b）2a2b3c]2；
（3）（x3）2÷x2÷x+x3÷（-x）2（-x2）； （4）(-9)3×( -
)3 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，DE⊥AD，交AB于点E，AE为⊙O的直径
（1）判断BC与⊙O的位置关系，并证明你的结论；
（2）求证：△ABD∽△DBE；
（3）若cosB=
，AE=4，求CD．
相关试题
