【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
(1)求证:BE是⊙O的切线;
(2)若BC=![]() ,AC=5,求圆的直径AD及切线BE的长.
,AC=5,求圆的直径AD及切线BE的长.
参考答案:
【答案】(1)详见解析;(2)R=3,BE=![]() .
.
【解析】
试题分析:(1)连接OB,根据已知条件易证∠EBD=∠CAB,继而得到∠BAD=∠EBD,根据直径所对的圆周角为直角即可证得结论;(2)连接CD,交OB于点F,易证OF为三角形ADC的中位线,根据三角形的中位线定理求得OF,再用平行线分线段成比例定理求出半径R,最后用切割线定理即可.
试题解析:(1)如图,
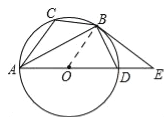
连接OB,∵BD=BC,
∴∠CAB=∠BAD,
∵∠EBD=∠CAB,
∴∠BAD=∠EBD,
∵AD是⊙O的直径,
∴∠ABD=90°,OA=BO,
∴∠BAD=∠ABO,
∴∠EBD=∠ABO,
∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,
∵点B在⊙O上,
∴BE是⊙O的切线,
(2)如图2,
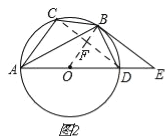
设圆的半径为R,连接CD,
∵AD为⊙O的直径,
∴∠ACCD=90°,
∵BC=BD,
∴OB⊥CD,
∴OB∥AC,
∵OA=OD,
∴OF=![]() AC=
AC=![]() ,
,
∵四边形ACBD是圆内接四边形,
∴∠BDE=∠ACB,
∵∠DBE=∠ACB,
∴△DBE∽△CAB,
∴![]() ,
,
即![]() ,
,
∴DE=![]() ,
,
∵∠OBE=∠OFD=90°,
∴DF∥BE,
∴![]() ,
,
∴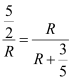 ,
,
∵R>0,
∴R=3,
∵BE是⊙O的切线,
∴BE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a=a3成立,则a可能的取值有( )
A. 1个 B. 2个 C. 3个 D. 无数个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中既是中心对称图形,又是轴对称图形的是( )
A.正三角形B.平行四边形C.等腰梯形D.正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x+2y=5,则代数式3﹣x﹣2y的值为( )
A.﹣8B.﹣2C.2D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题7分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.
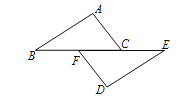
(1)选择的条件是 (填序号)
(2)证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“两条等弧所对的两条弦相等”的逆命题是________命题(填“真”或“假”).
-
科目: 来源: 题型:
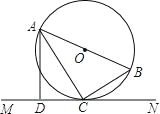
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD=30°,求⊙O的半径.
相关试题

