【题目】数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.已知数轴上有点A和点B,点A和点B分别表示数-20和40,请解决以下问题:
(1)请画出数轴,并标明A、B两点;
(2)若点P、Q分别从点A、点B同时出发,相向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点C时,C所对应的数是多少?
(3)若点P、Q分别从点A、点B同时出发,沿x轴正方向同向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点D时,D所对应的数是多少?
参考答案:
【答案】(1)见解析:(2)20;(3)100.
【解析】
根据题意画出数轴,标出A、B两点即可;
设运动x秒后,P、Q两点相遇,列出方程解出x的值即可求;
设运动y秒后,P、Q两点相遇,列出方程解出y的值即可求.
解:(1)

(2)设运动x秒后,P、Q两点相遇,根据题意得
4x+2x=40-(-20)
解得x=10
-20+4×10=-20+40=20,点C对应的数为20.
(3) 设运动y秒后,P、Q两点相遇,根据题意得
4y-2y=40-(-20)
解得y=30.
-20+4×30=-20+120=100,所以点D对应的数为100.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.

(1)求证:△CDE∽△CAD;
(2)若AB=2,AC=2 ,求AE的长.
,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价y1(元/台)与采购数量x1(台)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).
(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的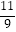 ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?
(2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2 , 线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连接AP、CE.
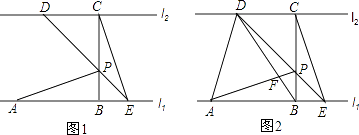
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F.如图2.
①当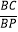 =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;
②当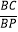 =n(n>1)时,设△PAD的面积为S1 , △PCE的面积为S2 , 求
=n(n>1)时,设△PAD的面积为S1 , △PCE的面积为S2 , 求 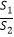 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
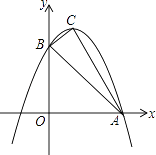
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S. -
科目: 来源: 题型:
查看答案和解析>>【题目】当n为1,2,3,…时,由大小相同的小正方形组成的图形如图所示,则第10个图形中小正方形的个数总和等于( )
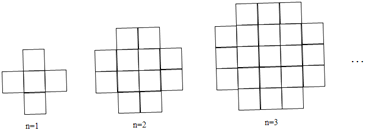
A. 100 B. 96 C. 144 D. 140
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数1至2019按一定规律排列如下表:
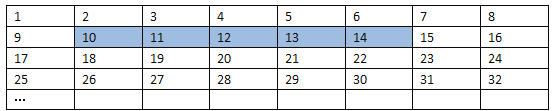
平移表中带阴影的方框,则方框中五个数的和可以是( )
A. 2010 B. 2018 C. 2019 D. 2020
相关试题

