【题目】为了解某校九年级学生的身高情况,随机抽取了部分学生的身高进行调查,利用所得数据绘成如下统计图表:
频数分布表
身高分组/cm | 频数 | 百分比 |
| 5 | 10% |
| 20% | |
| 15 | 30% |
| 14 | |
| 6 | 12% |
总计 | 100% |
(1)填空:![]() ______;
______;
(2)通过计算补全频数分布直方图;
(3)该校九年级一共有600名学生,估计身高不低于165cm的学生大约有多少人?

参考答案:
【答案】(1)28%;(2)见解析;(3)该校九年级共有600名学生,身高不低于165cm的学生大约有240人
【解析】
(1)用x<155的频数除以所占百分比可以求得调查的学生总数,从而可以求得a的值;
(2)用155≤x<160所占的百分比乘以总人数得到155≤x<160的人数,从而补全频数分布直方图;
(3)用九年级总人数乘以身高不低于165cm的学生所占的百分比即可.
解:(1)由表格可得,调查的总人数为:5÷10%=50,
a=14÷50×100%=28%,
故答案是:28%;
(2)155≤x<160的人数是:50×20%=10(人),补图如下: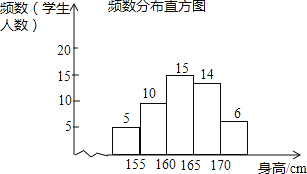
(3)根据题意得:
600×(28%+12%)=600×40%=240(人)
即该校九年级共有600名学生,身高不低于165cm的学生大约有240人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感.他惊喜的发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:
(1)将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°.求证:a2+b2=c2.
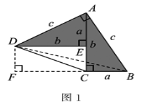
(2)请参照上述证法,利用图2完成下面的证明.
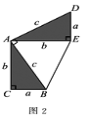
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证:a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程mx2﹣(m+2)x+2=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学在一次实验中统计了某一结果出现的频率,给出的统计图如图所示,则 符合这一结果的实验可能是( )

A. 掷一枚正六面体的骰子,出现6点的概率
B. 掷一枚硬币,出现正面朝上的概率
C. 任意写出一个整数,能被2整除的概率
D. 一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程(组):
(1)
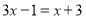
(2)
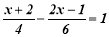
(3)
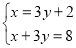
(4)
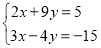
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在五一期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且余30个座位.
(1)求外出旅游的学生人数是多少,单租45座的客车需多少辆?
(2)已知45座的客车每辆租金250元,60座的客车每辆租金300元,为节省租金,并且保证每个学生都有座,决定同时租用两种客车,使得租车总数比单租45座的客车少一辆,问45座的客车和60座的客车分别租多少辆才能使得租金最少?
相关试题

