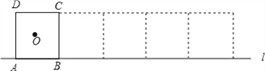
【题目】如图,将边长为1,中心为点O的正方形ABCD在直线l上按顺时针方向不滑动地每秒转动90°.
(1)第1秒点O经过的路线长为______,第2秒点O经过的路线长为______,第2013秒点O经过的路线长为______.
(2)分别求出第1秒、第2秒、第2013秒点A经过的路线长.
参考答案:
【答案】(1) ![]() π;
π; ![]() π;
π; ![]() π;(2)
π;(2) ![]() π;
π; ![]() π;
π; ![]() π;
π;
【解析】试题分析:(1)第1秒点O经过的路线长为以点B为圆心,OB长为半径,90°的圆弧;第2秒点O经过的路线长为以点C为圆心,OC长为半径,90°的圆弧,根据弧长公式计算即可,正方形每秒都要翻滚90°,翻转一周共四次,一共翻滚360°,算出OC的长等于![]() ,再求出正方形的中心O所经过的路径长;
,再求出正方形的中心O所经过的路径长;
(2)第1秒点A经过的路线长为以点B为圆心,AB长为半径,90°的圆弧,第2秒是C点为圆心CA为半径,第三秒D点为圆心DA为半径,第四秒A为圆心路径为0,4秒一个大周期,根据弧长公式计算即可.
试题解析:解:(1)∵AB=1,∴OC=![]() ,∴第1秒点O经过的路线长为
,∴第1秒点O经过的路线长为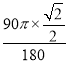 =
=![]() π,第2秒点O经过的路线长为
π,第2秒点O经过的路线长为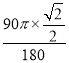 =
=![]() π,第2013秒点O经过的路线长为
π,第2013秒点O经过的路线长为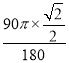 =
=![]() π,故答案为:
π,故答案为: ![]() π,
π, ![]() π,
π, ![]() π;
π;
(2)第1秒点A经过的路线长为![]() =
=![]() π,第2秒点A经过的路线长为
π,第2秒点A经过的路线长为![]() =
=![]() π,第2013秒点A经过的路线长为
π,第2013秒点A经过的路线长为![]() =
=![]() π.
π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(a2)3=( )
A.a6B.a5C.a3D.a﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABC D,E为平面内任意一点,连接AE,BE,将△ABE绕点B顺时针旋转90°得到△BFC.
(1)如图1,求证:①
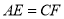 ;②
;②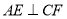 .
.(2)若
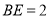 ,
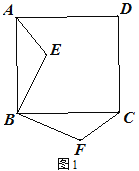
,① 如图2,点E在正方形内,连接EC,若
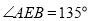 ,
, 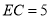 ,求
,求 的长;
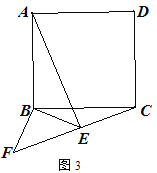
的长;② 如图3,点E在正方形外,连接EF,若AB=6,当C、E、F在一条直线时,
求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上.(每个小方格的顶点叫格点)

(1)画出△ABC向下平移3个单位后的△A1B1C1;
(2)画出△ABC绕点O顺时针旋转90°后的△A2B2C2,并求点A旋转到A2所经过的路线长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2a4=a8B.(2a2)2=2a4C.a2÷(﹣a)2=1D.(﹣a2)3=a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2x=a,2y=b,则2x+y=( )
A.a+bB.abC.abD.ba
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000元;经粗加工后销售,每吨利润可达4 500元;经精加工后销售,每吨利润涨至7 500元.
当地一家蔬菜公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司制订了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
相关试题

