【题目】如图,![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 中点,若
中点,若![]() 的周长为28,
的周长为28,![]() ,则
,则![]() 的周长为( )
的周长为( )
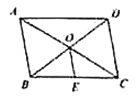
A.12B.17C.19D.24
参考答案:
【答案】A
【解析】
由四边形ABCD是平行四边形,根据平行四边形的性质可得OB=OD,再由E是CD中点,即可得BE=![]() BC,OE是△BCD的中位线,由三角形的中位线定理可得OE=
BC,OE是△BCD的中位线,由三角形的中位线定理可得OE=![]() AB, 再由ABCD的周长为28,BD=10, 即可求得AB+BC=14,BO=5,由此可得BE+OE=7, 再由△OBE的周长为=BE+OE+BO即可求得△OBE的周长.
AB, 再由ABCD的周长为28,BD=10, 即可求得AB+BC=14,BO=5,由此可得BE+OE=7, 再由△OBE的周长为=BE+OE+BO即可求得△OBE的周长.
∵四边形ABCD是平行四边形,
∴O是BD中点, OB=OD,
又∵E是CD中点,
∴BE=![]() BC,OE是△BCD的中位线,
BC,OE是△BCD的中位线,
∴OE=![]() AB,
AB,
∵ABCD的周长为28,BD=10,
∴AB+BC=14,
∴BE+OE=7,BO=5
∴△OBE的周长为=BE+OE+BO=7+5=12.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,-4) ,B(3,-3) ,C(1,-1).(每个小方格都是边长为一个单位长度的正方形)
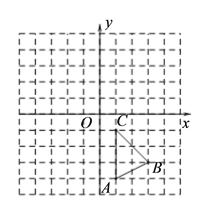
(1)将△ABC沿y轴方向向上平移5个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕点O顺时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点A旋转到点A2所经过的路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.下图反映了这个过程,小明离家的距离
 与时间
与时间 之间的对应关系.根据图象,下列说法中正确的是( )
之间的对应关系.根据图象,下列说法中正确的是( )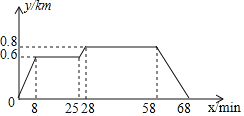
A. 小明吃早餐用了25分钟
B. 食堂到图书馆的距离为
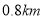
C. 小明读报用了30分钟
D. 小明从图书馆回家的平均速度为
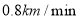
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两汽车从A市出发,丙汽车从B市出发,甲车每小时行驶40千米,乙车每小时行驶45千米,丙车每小时行驶50千米,如果三辆汽车同时相向而行,丙车遇到乙车后10分钟才能遇到甲车,问何时甲丙两车相距15千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=150,∠AOC=40,OE是∠AOB内部的一条射线,OF平分∠AOE, 且OF在OC的右侧.
(1)若∠EOB=10,求∠COF的度数;
(2)若∠COF=20,求∠EOB的度数;
(3)若∠COF=n,求∠EOB的度数(用含n的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个有理数的和等于这两个有理数的积,则称这两个有理数互为相依数.例如:有理数
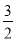 与3,因为
与3,因为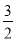 +3=
+3=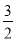 ×3.所以有理数与
×3.所以有理数与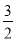 与3是互为相依数.
与3是互为相依数.(1)直接判断下列两组有理数是否互为相依数,
①-5与-2;②-3与
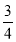 ;
;(2)若有理数
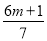 与-7 互为相依数,求m的值;
与-7 互为相依数,求m的值;(3)若有理数a与b互为相依数,b与c互为相反数,求式子5(ab+
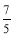 c)-2(
c)-2(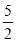 a-b)-4的值;
a-b)-4的值;(4)对于有理数a(a≠0,1),对它进行如下操作:取a的相依数,得到a1;取a1的倒数,得到a2;取a2的相依数,得到a3;取a3的倒数,得到a4;…,;依次按如上的操作得到一组数a1,a2,a3,…,an , 若a=
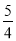 ,试着直接写出a1,a2,a3,…, a2018的和.
,试着直接写出a1,a2,a3,…, a2018的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱剩余油量为30升.(假设行驶过程中汽车的耗油量是均匀的.)
(1)写出用行驶路程x(千米)来表示剩余油量Q(升)的代数式;
(2)当x=300千米时,求剩余油量Q的值;
(3)当油箱中剩余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
相关试题

