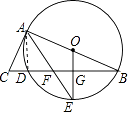
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是BD弧上的一点,OE⊥BD于点G,连接AE交BC于点F,AC是⊙O的切线. 
(1)求证:∠ACB=2∠EAB;
(2)若cos∠ACB= ![]() ,AC=10,求BF的长.
,AC=10,求BF的长.
参考答案:
【答案】
(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵AC是⊙O的切线,
∴∠CAB=90°,
∴∠C+∠CAD=∠CAD+∠DAB=90°,
∴∠C=∠DAB,
∵OE⊥BD,
∴2 ![]() =
= ![]() ,
,
∴∠BAE= ![]() BDA,
BDA,
∴∠ACB=2∠EAB
(2)解:∵cos∠ACB= ![]() ,AC=10,
,AC=10,
∴BC=25,
∴AB= ![]() =5
=5 ![]() ,
,
∵∠C=∠BAD,∠B=∠B,
∴△ABC∽△DBA,
∴ ![]() ,
,
∴BD= ![]() =21,
=21,
∵OE⊥BD,
∴BG=DG= ![]() ,
,
∵AD= ![]() =2
=2 ![]() ,
,
∵AO=BO,BG=DG,
∴OG= ![]() AD=
AD= ![]() ,
,
∴GE= ![]() ,
,
∵AD∥GE,
∴ ![]() =
= ![]() ,
,
∴FG= ![]() DG=
DG= ![]() ,
,
∴BF=BG+FG= ![]() +
+ ![]() =15.
=15.
【解析】(1)连接AD,由AB是⊙O的直径,得到∠ADB=90°,由AC是⊙O的切线,得到∠CAB=90°,根据余角的性质得到∠C=∠DAB,根据圆周角定理即可得到结论;(2)根据三角函数的定义得到BC=25,根据勾股定理得到AB= ![]() =5
=5 ![]() ,根据相似三角形的性质得到BD=
,根据相似三角形的性质得到BD= ![]() =21,根据垂径定理得到BG=DG=
=21,根据垂径定理得到BG=DG= ![]() ,根据平行线分线段成比例定理得到
,根据平行线分线段成比例定理得到 ![]() =
= ![]() ,于是得到结论.
,于是得到结论.
【考点精析】本题主要考查了垂径定理和切线的性质定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】去年6月某日自治区部分市、县的最高气温(℃)如下表:
区县
吐鲁番
塔城
和田
伊宁
库尔勒
阿克苏
昌吉
呼图壁
鄯善
哈密
气温(℃)
33
32
32
30
30
29
29
31
30
28
则这10个市、县该日最高气温的众数和中位数分别是( )
A.32,32
B.32,30
C.30,30
D.30,32 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )

A.AD=AB
B.∠BOC=2∠D
C.∠D+∠BOC=90°
D.∠D=∠B -
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.
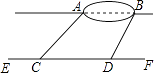
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系xOy中,一次函数y=﹣x+b(b为常数,b>0)的图象与x轴、y轴分别交于A、B两点,半径为5的圆⊙O与x轴正半轴相交于点C,与y轴相交于D、E两点.
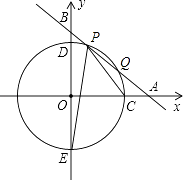
(1)若直线AB交劣弧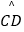 于P、Q两点(异于C、D)
于P、Q两点(异于C、D)
①当P点坐标为(3,4)时,求b值;
②求∠CPE的度数,并用含b的代数式表示弦PQ的长(写出b的取值范围);
(2)当b=6时,线段AB上存在几个点F,使∠CFE=45°?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的顶点B在反比例函数
 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( )
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( ) 
A.12
B.4
C.12-3
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使DA与对角线DB重合,点A落在点A′处,折痕为DE,则A′E的长是 .

相关试题

