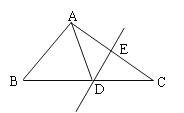
【题目】如图,在△ABC中,DE是AC的垂直平分线.
(1)若AE=6,则AC= ;
(2)若∠ABD=40,∠ADB=70,求∠BAC的度数.
参考答案:
【答案】(1)12;(2)∠BAC=105°
【解析】试题分析:(1)由线段垂直平分线的性质可得:AE=CE,即可求得AC值;
(2)由线段垂直平分线的性质得DA=DC,由等边对等角,得∠DAC=∠C,由外角的性质,可求得∠C=35°,再由三角形外角和定理可得∠BAC度数.
试题解析:(1)∵DE是AC的垂直平分线,
∴AE=CE=6,
∴AC=2AE=12;
故答案为:12;
(2) ∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DAC=∠C,
又∵∠ADB为△ADC的外角,
∴∠DAC+∠C=∠ADB=70,
∴∠DAC=∠C=35°,
在△ABC中,∠BAC+∠ABD+∠C=180°.
∴∠BAC=180°-∠ABD-∠C=180°-40-35°=105°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程(组):(1)
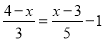 ;(2)
;(2)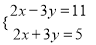
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF=cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°.
(1)已知c=25,b=15,求a;
(2)已知a=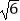 ,∠A=60°,求b、c.
,∠A=60°,求b、c. -
科目: 来源: 题型:
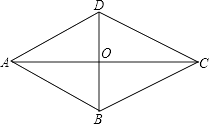
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算: ①(x+2)(x﹣4)
②(x+2)(x﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件为必然事件的是( )
A.打开电视,正在播放新闻B.买一张电影票,座位号是奇数号
C.任意画一个三角形,其内角和是180°D.掷一枚质地均匀的硬币,正面朝上
相关试题

