搜索
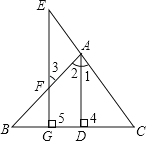
【题目】已知：如图，AD⊥BC于D，EG⊥BC与G，∠E=∠3，试问：AD是∠BAC的平分线吗？若是，请说明理由．
解答：是，理由如下：
∵AD⊥BC，EG⊥BC（已知）
∴∠4=∠5=90°（垂直的定义）
∴AD∥EG
∴∠1=∠E
∠2=∠3
∵∠E=∠3（已知）
∴ =
∴AD是∠BAC的平分线（角平分线的定义）．
参考答案：
【答案】同位角相等，两直线平行，两直线平行，同位角相等，两直线平行，内错角相等，∠1，∠2
【解析】解：是．
∵AD⊥BC，EG⊥BC（已知）
∴∠4=∠5=90°（垂直的定义）
∴AD∥EG，（同位角相等，两直线平行）
∴∠1=∠E，（两直线平行，同位角相等）
∠2=∠3．（两直线平行，内错角相等）
∵∠E=∠3，（已知）
∴∠1=∠2，
∴AD是∠BAC的平分线（角平分线的定义）．
故答案为：同位角相等，两直线平行，两直线平行，同位角相等，两直线平行，内错角相等，∠1，∠2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某家禽养殖场，用总长为110m的围栏靠墙（墙长为22m）围成如图所示的三块矩形区域，矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半，设AD长为xm，矩形区域ABCD的面积为ym2．
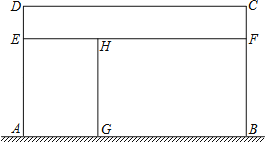
（1）求y与x之间的函数关系式，并写出自变量x的取值范围；
（2）当x为何值时，y有最大值？最大值是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在菱形ABCD中，对角线AC与BD相交于点O，MN过点O且与边AD、BC分别交于点M和点N．
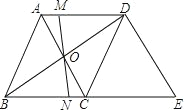
（1）请你判断OM与ON的数量关系，并说明理由；
（2）过点D作DE∥AC交BC的延长线于E，当AB=5，AC=6时，求△BDE的周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】体育文化用品商店购进篮球和排球共20个，进价和售价如表，全部销售完后共获利润260元．
篮球
排球
进价（元/个）
80
50
售价（元/个）
95
60
（1）购进篮球和排球各多少个？
（2）销售6个排球的利润与销售几个篮球的利润相等？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO=a°，则下列结论：
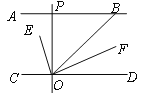
①∠BOE=
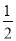（180-a）°；②OF平分∠BOD；③∠POE=∠BOF；④∠POB=2∠DOF．其中正确的个数有多少个？（ ）
A．1 B．2 C．3 D．4
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，矩形ABCD的对角线相交于点O，
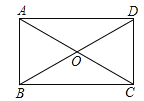
（1）若AB=2，∠AOD＝120,求对角线AC的长；
（2）若AC＝2AB．求证：△AOB是等边三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】2016年山东省高考报名人数位居全国第三，约有696000人报名，将696000用科学记数法表示为（ ）
A.69.6×104
B.6.96×105
C.6.96×106
D.0.696×106
相关试题
