【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动. 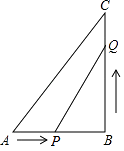
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于2 ![]() cm?
cm?
(3)在(1)中,△PQB的面积能否等于7cm2?说明理由.
参考答案:
【答案】
(1)解:设经过x秒以后△PBQ面积为4cm2,根据题意得 ![]() (5﹣x)×2x=4,
(5﹣x)×2x=4,
整理得:x2﹣5x+4=0,
解得:x=1或x=4(舍去).
答:1秒后△PBQ的面积等于4cm2
(2)解:PQ=2 ![]() ,则PQ2=25=BP2+BQ2,即40=(5﹣t)2+(2t)2,
,则PQ2=25=BP2+BQ2,即40=(5﹣t)2+(2t)2,
解得:t=0(舍去)或3.
则3秒后,PQ的长度为2 ![]() cm
cm
(3)解:令S△PQB=7,即BP× ![]() =7,(5﹣t)×
=7,(5﹣t)× ![]() =7,
=7,
整理得:t2﹣5t+7=0,
由于b2﹣4ac=25﹣28=﹣3<0,
则原方程没有实数根,
所以在(1)中,△PQB的面积不能等于7cm2
【解析】(1)经过x秒钟,△PBQ的面积等于4cm2 , 根据点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,表示出BP和BQ的长可列方程求解;(2)利用勾股定理列出方程求解即可;(3)令S△PQB=7,根据三角形的面积公式列出方程,再根据b2﹣4ac得出原方程没有实数根,从而得出△PQB的面积不能等于7cm2 .
【考点精析】掌握勾股定理的概念是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 过一点有且只有一条直线与已知直线平行
B. 不相交的两条直线叫做平行线
C. 两点确定一条直线
D. 两点间的距离是指连接两点间的线段
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a+3|+|b﹣1|=0,则ab的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,求1+2-1+2-2+…+2-2 016的值.
解:设S=1+2-1+2-2+…+2-2016, ①
则2S=2+1+2-1+…+2-2 015, ②
②-①得S=2-2-2 016.
请你仿此计算:
(1)1+3-1+3-2+…+3-2 016;
(2)1+3-1+3-2+…+3-n(n为正整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果正确的是( )
A.a2+a3=a5
B.a2a3=a6
C.a3÷a2=a
D.(a2)3=a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y1=ax2+bx+c的对称轴是x=3,与x轴的一个交点为(5,0);它与直线y2=mx+n的图象如图所示,下列判断中:①abc<0;②a+b+c>0;③5a﹣c=0; ④当
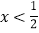 或
或 时,y1>y2,其中正确的个数有
时,y1>y2,其中正确的个数有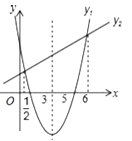
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各对数中,互为相反数的是( )
A.﹣(﹣3)和+(+3)B.﹣(+3)和+(﹣3)
C.﹣(+3)和+(+3)D.﹣(﹣3)和3
相关试题

