【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.

(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)由DE∥AC和AE∥BD得到:四边形AODE是平行四边形,由菱形ABCD中AC和BD是对角线得到:AC⊥BD,综合以上两点可得平行四边形AODE是矩形;(2)由∠BCD=120°,AB∥CD得:∠ABC=180°﹣120°=60°,又因为AB=BC得:△ABC是等边三角形,所以OA=![]() ×4=2,在菱形ABCD中,AC⊥BD,由勾股定理OB=
×4=2,在菱形ABCD中,AC⊥BD,由勾股定理OB=![]() ,由四边形ABCD是菱形得:OD=OB=
,由四边形ABCD是菱形得:OD=OB=![]() ,所以四边形AODE的面积=OAOD=2
,所以四边形AODE的面积=OAOD=2![]() (或
(或![]() );
);
试题解析:
(1)∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是矩形,
故,四边形AODE是矩形;
(2)∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=![]() ×4=2,
×4=2,
∵在菱形ABCD中,AC⊥BD
∴由勾股定理OB=![]()
∵四边形ABCD是菱形,
∴OD=OB=![]() ,
,
∴四边形AODE的面积=OAOD=2![]() (或
(或![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE∥BF,AC平分∠BAE,交BF于C.

(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)求证:AD=BC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不超过8 000元,那么该商店至多购进A种纪念品几件? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
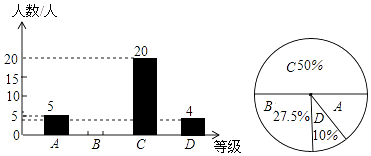
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】有一种公益叫“光盘”.所谓“光盘”,就是吃光你盘子中的食物,杜绝“舌尖上的浪费”.某校九年级开展“光盘行动”宣传活动,根据各班级参加该活动的总人次折线统计图,下列说法正确的是( )

A. 极差是40 B. 中位数是58 C. 平均数大于58 D. 众数是5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某班参加课外活动的总共有30人,跳绳的人数占30%,表示踢毽的扇形圆心角是60°,踢毽和打篮球的人数比是1:2,那么参加“其它”活动的人数有________人.

相关试题

