【题目】已知:在Rt△ABC中,AB=BC;在Rt△ADE中,AD=DE;连结EC,取EC的中点M,连结DM和BM.
(1)若点D在边AC上,点E在边AB上且与点B不重合,如图①,
求证:BM=DM且BM⊥DM;
(2)如果将图①中的△ADE绕点A逆时针旋转小于45°的角,如图②,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.
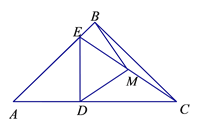

图① 图②
参考答案:
【答案】(1)证明见解析(2)当△ADE绕点A逆时针旋转小于45°的角时,(1)中的结论成立
【解析】分析:(1)、根据直角三角形斜边上的中线的性质得出BM=DM,然后根据四点共圆可以得出∠BMD=2∠ACB=90°,从而得出答案;(2)、连结BD,延长DM至点F,使得DM=MF,连结BF、FC,延长ED交AC于点H,根据题意得出四边形CDEF为平行四边形,然后根据题意得出△ABD和△CBF全等,根据角度之间的关系得出∠DBF=∠ABC =90°.
详解:(1)在Rt△EBC中,M是斜边EC的中点,∴![]() .
.
在Rt△EDC中,M是斜边EC的中点,∴![]() .
.
∴BM=DM,且点B、C、D、E在以点M为圆心、BM为半径的圆上.
∴∠BMD=2∠ACB=90°,即BM⊥DM.
(2)当△ADE绕点A逆时针旋转小于45°的角时,(1)中的结论成立.
证明:连结BD,延长DM至点F,使得DM=MF,连结BF、FC,延长ED交AC于点H.
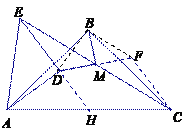
∵ DM=MF,EM=MC, ∴ 四边形CDEF为平行四边形,∴ DE∥CF ,ED =CF,
∵ ED= AD,∴ AD=CF, ∵ DE∥CF,∴ ∠AHE=∠ACF.
∵![]() ,
,![]() ,
,
∴ ∠BAD=∠BCF, 又∵AB= BC, ∴ △ABD≌△CBF,∴ BD=BF,∠ABD=∠CBF,
∵ ∠ABD+∠DBC =∠CBF+∠DBC,∴∠DBF=∠ABC =90°.
在Rt△![]() 中,由
中,由![]() ,
, ![]() ,得BM=DM且BM⊥DM.
,得BM=DM且BM⊥DM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年8月,我国空军八一飞行表演队赴俄罗斯国际军事技术论坛上进行飞行表演,其中一架飞机起飞后的高度变化如下表:

(1) 如果飞机每上升或下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
(2) 如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.8千米,下降2.9千米,再上升1.6千米.若要使飞机最终比起飞点高出1千米,问第4个动作是上升还是下降,上升或下降多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
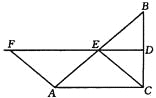
(1)求证:四边形ACEF是平行四边形;
(2)当∠B的大小满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论;
(3)四边形ACEF有可能是正方形吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线y=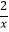 上的概率.
上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若
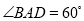 ,AB=2,则图中阴影部分的面积为( )
,AB=2,则图中阴影部分的面积为( )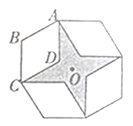
A. 12-4
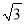 B. 5 C. 12-4
B. 5 C. 12-4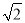 D. 6
D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.
(1)求证:四边形CMAN是平行四边形.
(2)已知DE=2,FN=1,求BN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴子A、B两点,与反比例函数y
 的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.(1)求反比例函数与一次函数的关系式;
(2)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?

相关试题

