【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[﹣2.5]=﹣3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4>=5,<﹣1.5>=﹣1.解决下列问题:
(1)[﹣4.5]=________,<3.5>=________.
(2)若[x]=2,则x的取值范围是________;若<y>=﹣1,则y的取值范围是________.
(3)已知x,y满足方程组 ,求x,y的取值范围.
,求x,y的取值范围.
参考答案:
【答案】(1)﹣5;4;(2)2≤x<3;﹣2≤y<﹣1(3)﹣1≤x<0,2≤y<3
【解析】试题分析:(1)根据题目条件:用[a]表示不大于a的最大整数,用<a>表示大于a的最小整数,可分别求解;(2)根据[a]表示不大于a的最大整数,可得[x]=2中的2≤x<3,根据<a>表示大于a的最小整数,可得<y>=-1中,-2≤y<-1;(3)先解方程组,求出[x]和<y>的值,然后求出x和y的取值范围.
试题解析:1)由题意得,[-4.5]=-5,<3.5>=4;
(2)因为[a]表示不大于a的最大整数且[x]=2,所以x的取值范围是2≤x<3;
因为<a>表示大于a的最小整数,且<y>=-1, 所以y的取值范围是-2≤y<-1;
(3)解:解方程组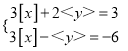 得:
得: ![]() ,
,
∴x,y的取值范围分别为﹣1≤x<0,2≤y<3
-
科目: 来源: 题型:
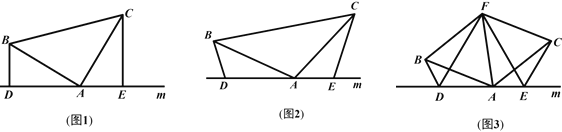
查看答案和解析>>【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点
互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“富春包子”是扬州特色早点,富春茶社为了了解顾客对各种早点的喜爱情况,设计了如右图的调查问卷,对顾客进行了抽样调查.根据统计数据绘制了如下尚不完整的统计图.

根据以上信息,解决下列问题:
(1)条形统计图中“汤包”的人数是 ,扇形统计图中“蟹黄包”部分的圆心角为 °;
(2)根据抽样调查结果,请你估计富春茶社1000名顾客中喜欢“汤包”的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,不正确的是( )
A.m3+m3=m6B.m4m=m5C.m6÷m2=m4D.(m5)2=m10
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程是一元一次方程的是( )
A.2x+1=0B.3x+2y=5C.xy+2=3D.x2=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=4是关于x的不等式x﹣3m+2≤0的解,则m的取值范围为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC;
②若半圆O的半径为12,求阴影部分的周长.

相关试题

