【题目】一个角补角比它的余角的2倍多30°,求这个角的度数.
参考答案:
【答案】解:设这个角为x,
由题意得,180°﹣x=2(90°﹣x)+30°,
解得x=30°.
答:这个角的度数是30°
【解析】设这个角为x,根据余角和补角的概念列出方程,解方程即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.
(1)如图1,求证:ED为⊙O的切线;
(2)如图2,直线ED与切线AG相交于G,且OF=1,⊙O的半径为3,求AG的长.
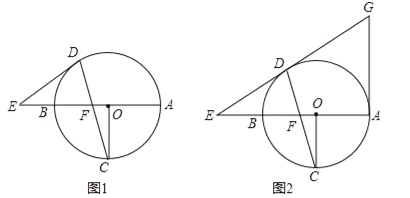
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题提出】
学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”) 和直角三角形全等的判定方法(即“HL”) 后, 我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
不妨将问题用符号语言表示为: 在△ABC和△DEF中, AC = DF, BC = EF, ∠B =∠E,
然后, 对∠B进行分类, 可分为“∠B是直角、钝角、锐角”三种情况进行探究.
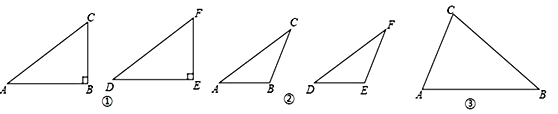
【深入探究】
第一种情况: 当∠B是直角时, △ABC≌△DEF.
(1) 如图①, 在△ABC和△DEF, AC = DF, BC = EF, ∠B =∠E = 90°, 根据_____________, 可以知道Rt△ABC≌Rt△DEF.
第二种情况: 当∠B是钝角时, △ABC≌△DEF.
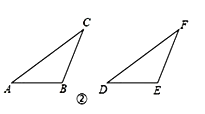
(2) 如图②, 在△ABC和△DEF, AC = DF, BC = EF, ∠B =∠E, 且∠B、∠E都是钝角.
求证: △ABC≌△DEF.
第三种情况: 当∠B是锐角时, △ABC和△DEF不一定全等.
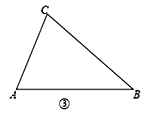
(3) 在△ABC和△DEF, AC = DF, BC = EF, ∠B = ∠E, 且∠B、∠E都是锐角, 请你用尺规在图③中作出△DEF, 使△DEF和△ABC不全等. (不写作法, 保留作图痕迹)
(4) ∠B还要满足什么条件, 就可以使△ABC≌△DEF ? 请直接写出结论: 在△ABC和△DEF中, AC = DF, BC = EF, ∠B =∠E, 且∠B、∠E都是锐角, 若__________, 则△ABC≌△DEF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:2(x﹣3)2=x2﹣9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次英语测试后,随机抽取九年级某班5名学生的成绩如下:91,78,98,85,98.关于这组数据众数是( )
A.众数是91
B.众数是78
C.众数是98
D.众数是85 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察列数:﹣2,8,﹣32,128……按照这列数的排列规律,第n个数应该是( )
A.(﹣2)nB.(﹣2)2n﹣1C.﹣22n﹣1D.(﹣1)n22n﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是( )

A.点M在AB上
B.点M在BC的中点处
C.点M在BC上,且距点B较近,距点C较远
D.点M在BC上,且距点C较近,距点B较远
相关试题

