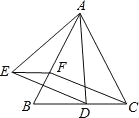
【题目】如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)由△ABC是等边三角形得到∠B=60°,而∠EFB=60°,由此可以证明EF∥DC,而DC=EF,然后即可证明四边形EFCD是平行四边形;
(2)如图,连接BE,由BF=EF,∠EFB=60°可以推出△EFB是等边三角形,然后得到EB=EF,∠EBF=60°,而DC=EF,由此得到EB=DC,又
△ABC是等边三角形,所以得到∠ACB=60°,AB=AC,然后即可证明△AEB≌△ADC,利用全等三角形的性质就证明AE=AD.
试题解析:(1)∵△ABC是等边三角形,
∴∠ABC=60°,
∵∠EFB=60°,
∴∠ABC=∠EFB,
∴EF∥DC(内错角相等,两直线平行),
∵DC=EF,
∴四边形EFCD是平行四边形;
(2)连接BE
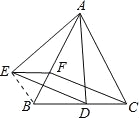
∵BF=EF,∠EFB=60°,
∴△EFB是等边三角形,
∴EB=EF,∠EBF=60°
∵DC=EF,
∴EB=DC,
∵△ABC是等边三角形,
∴∠ACB=60°,AB=AC,
∴∠EBF=∠ACB,
∴△AEB≌△ADC,
∴AE=AD.
-
科目: 来源: 题型:
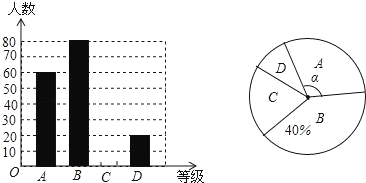
查看答案和解析>>【题目】“切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外作业时间,随机抽取部分学生进行问卷调查,并将调查结果分为A、B、C、D四个等级,A:1小时以内;B:1小时--1.5小时;C:1.5小时--2小时;D:2小时以上.根据调查结果绘制了如图所示的两种不完整的统计图,请根据图中信息解答下列问题:
(1)该校共调查了 学生;
(2)请将条形统计图补充完整;
(3)表示等级A的扇形圆心角α的度数是 ;
(4)在此次调查问卷中,甲、乙两班各有2人平均每天课外作业量都是2小时以上,从这4人中人选2人去参加座谈,用列表表或画树状图的方法求选出的2人来自不同班级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论不正确的是( )
A. 若a>0,b<0,则a-b>0 B. 若a<0,b>0,则a-b<0
C. 若a<0,b<0,则a-(-b)>0 D. 若a<0,b<0,且|b|>|a|,则a-b>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a|=8,b=5,且a+b<0,那么a-b=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=∠C,∠B=∠D,则下列结论中错误的是( )
A.AB=CD
B.AD∥BC
C.∠A=∠B
D.对角线互相平分 -
科目: 来源: 题型:
查看答案和解析>>【题目】□ABCD中,∠A+∠C=100°,则∠B= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小敏离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示.请根据图象回答下列问题:
(1)小敏去超市途中的速度是 ;在超市逗留了 ;
(2)小敏几点几分返回到家?

相关试题

