【题目】某公路养护小组,乘车沿南北走向的公路巡察维护,如果规定向北为正,向南为负,某天的行驶记录如下:(单位:![]() )
)
+18,-9,+17,-14,-5,+12,-6,-7,+8,+15.
(1)养护小组最后到达的地方在出发点的哪个方向?离出发点多远?
(2)若汽车的油耗为![]() ,则这天汽车共耗油多少?
,则这天汽车共耗油多少?
参考答案:
【答案】(1)养护小组最后到达的地方在出发点的北方,距出发点29千米;
(2)这天汽车共耗油11.1升.
【解析】
(1)根据加法法则,将正数与正数相加,负数与负数相加,再根据正负数的意义得出答案.
(2)将各数的绝对值相加,再乘以单位油耗即可.
解:(1)(+18)+(-9)+(+17)+(-14)+(-5)+(+12)+(-6)+(-7)+(+8)+(+15)
=[-9+(-14)+(-5)+(-6)+(-7)]+(18+17+12+8+15)
=-41+70
=29.
答:养护小组最后到达的地方在出发点的北方,距出发点29千米;
(2)总行程为:
|+18|+|-9|+|+17|+|-14|+|-5|+|+12|+|-6|+|-7|+|+8|+|+15|
=18+9+17+14+12+5+6+8+7+15
=111.
∵每千米耗油01升,
∴总耗油为111×0.1=11.1升.
答:这天汽车共耗油11.1升.
-
科目: 来源: 题型:
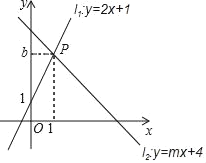
查看答案和解析>>【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值;
(2)垂直于x轴的直线与直线l1,l2,分别交于点C,D,垂足为点E,设点E的坐标为(a,0)若线段CD长为2,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲得分的方差比乙得分的方差小B. 甲得分的众数是8,乙得分的众数是9
C. 甲、乙得分的平均数都是8D. 甲得分的中位数是9,乙得分的中位数是6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,反比例函数
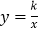 (x>0)的图象经过点A(
(x>0)的图象经过点A(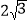 ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.(1)求k的值;
(2)求tan∠DAC的值及直线AC的解析式;
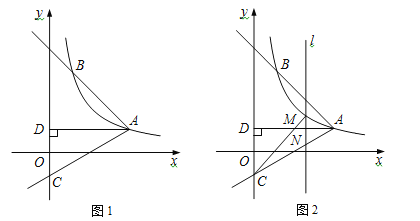
(3)如图2,M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,已知两车相遇时快车比慢车多行驶40千米,快车到达乙地时,慢车还有( )千米到达甲地.

A. 70 B. 80 C. 90 D. 100
-
科目: 来源: 题型:
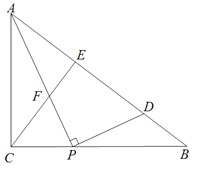
查看答案和解析>>【题目】如图,已知△ABC中,∠ACB=90°,AC=15,BC=20.动点P在线段CB上,以1cm/s的速度从点C向B运动,连接AP,作CE⊥AB分别交AP、AB于点F、E,过点P作PD⊥AP交AB于点D.
(1)线段CE= ;
(2)若t=5时,求证:△BPD≌△ACF;
(3)t为何值时,△PDB是等腰三角形;
(4)求D点经过的路径长.
-
科目: 来源: 题型:
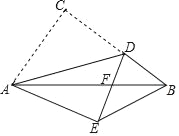
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为_____.
相关试题

