搜索
【题目】如图，∠D=∠C=90°，E是DC的中点，AE平分∠DAB，∠DEA=28°，则∠ABE的度数是（ ）
A. 62° B. 31° C. 28° D. 25°
参考答案：
【答案】C
【解析】如图，过点E作EF⊥AB于F，
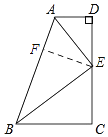
∵∠D=∠C=90°，AE平分∠DAB，
∴DE=EF，
∵E是DC的中点，
∴DE=CE，
∴CE=EF，
又∵∠C=90°，
∴点E在∠ABC的平分线上，
∴BE平分∠ABC，
又∵AD∥BC，
∴∠ABC+∠BAD=180°，
∴2∠BAE+2∠ABE=180°，
即∠BAE+∠ABE=90°
∴∠AEB=90°，
∴∠BEC=90°﹣∠AED=62°，
∴Rt△BCE中，∠CEB=62°，
∴∠CBE=28°，
∴∠ABE=∠CBE=28°．
故选C．
-
科目： 来源： 题型：
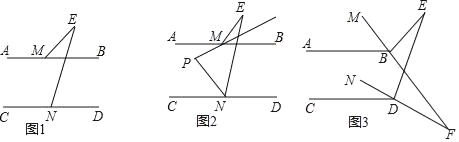
查看答案和解析>>【题目】已知直线AB∥CD．
（1）如图1，直接写出∠BME、∠E、∠END的数量关系为 ；
（2）如图2，∠BME与∠CNE的角平分线所在的直线相交于点P，试探究∠P与∠E之间的数量关系，并证明你的结论；
（3）如图3，∠ABM=
∠MBE，∠CDN=∠NDE，直线MB、ND交于点F，则
= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】三角形三条高的交点一定在（ ）
A.三角形的内部B.三角形的外部
C.顶点上D.以上三种情况都有可能
-
科目： 来源： 题型：
查看答案和解析>>【题目】某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．
（1）求每辆A型车和B型车的售价各为多少元．
（2）甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元．则有哪几种购车方案？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，大树AB与大数CD相距13m，小华从点B沿BC走向点C，行走一段时间后他到达点E，此时他仰望两棵大树的顶点A和D，两条视线的夹角正好为90°，且EA=ED.已知大树AB的高为5m，小华行走的速度为1m/s，小华行走到点E的时间是（ ）
A. 13s B. 8s C. 6s D. 5s
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列语句中正确的是（ ）
A.两个三角形的面积相等，那么这两个三角形全等
B.三个内角对应相等的两个三角形全等
C.两个等腰直角三角形全等，那么它们的斜边相等
D.两边及其中一边所对的角对应相等的两个三角形全等
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，对角线AC，BD相交于点O，点E，F分别在OA，OC上
（1）给出以下条件；①OB=OD，②∠1=∠2，③OE=OF，请你从中选取两个条件证明△BEO≌△DFO；
（2）在（1）条件中你所选条件的前提下，添加AE=CF，求证：四边形ABCD是平行四边形．
相关试题
