【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)

参考答案:
【答案】(2![]() +4)米.
+4)米.
【解析】
试题分析:延长AD交BC的延长线于E,作DF⊥BE于F,根据直角三角形的性质和勾股定理求出DF、CF的长,根据正切的定义求出EF,得到BE的长,根据正切的定义解答即可.
试题解析:延长AD交BC的延长线于E,作DF⊥BE于F,
∵∠BCD=150°,
∴∠DCF=30°,又CD=4,
∴DF=2,CF=![]() =2
=2![]() ,
,
由题意得∠E=30°,
∴EF=![]() =2
=2![]() ,
,
∴BE=BC+CF+EF=6+4![]() ,
,
∴AB=BE×tanE=(6+4![]() )×
)×![]() =(2
=(2![]() +4)米,
+4)米,
答:电线杆的高度为(2![]() +4)米.
+4)米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一种新型病毒的直径约为0.000043毫米,用科学记数法表示为( )毫米.
A. 0.43×10-4 B. 0.43×10-5 C. 4.3×10-5 D. 4.3×10-8
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
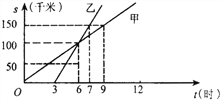
(1)此变化过程中,__________是自变量,_________是因变量.
(2)甲的速度是 ________千米/时,乙的速度是________千米/时
(3)9时甲在乙的________(前面、后面、相同位置)
(4)6时表示____________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.

(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某事件经过500000000次试验,出现的频率是0.3,它的概率估计值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】x2+ax+b分解因式的结果是(x﹣1)(x+2),则方程x2+ax+b=0的二根分别是什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A的坐标(a,b)满足条件(a+3)2+|b﹣2|=0,则点A在第象限.
相关试题

