【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上: .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别![]() a、
a、![]() a、
a、![]() a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.

参考答案:
【答案】(1)3.5;(2)见解析;(3)3a2
【解析】
(1)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解;
(2)分别找到A、B、C关于直线EF的对称点MNG,顺次连接各点即可;
(3)先作出以a、2a为直角边的三角形的斜边,再根据勾股定理和网格结构作出![]() a、
a、![]() a的长度,然后顺次连接即可;再根据三角形所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
a的长度,然后顺次连接即可;再根据三角形所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
(1)△ABC的面积=3×3-![]() ×1×2
×1×2![]() ×1×3
×1×3![]() ×2×3=9-1-
×2×3=9-1-![]() -3=9-5.5=3.5;
-3=9-5.5=3.5;
故答案为:3.5;
(2)△MNG如图所示:

(3)△ABC如图所示,

△ABC的面积=2a·4a-![]() ×2a·a-
×2a·a-![]() ×2a·2a-
×2a·2a-![]() ×4a·a=8a2-a2-2a2-2a2=3a2
×4a·a=8a2-a2-2a2-2a2=3a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了右图,如果继续“生长”下去 ,它将变得“枝繁叶茂”,请你算出“生长”了2018次后形成的图形中所有的正方形的面积和是( )

A. 2017 B. 2018 C. 2019 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是BC边上的高线,BE是一条角平分线,它们相交于点P , 已知∠EPD=125°,求∠BAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图:直线AB⊥BC,四边形ABCD是正方形,且AB=6,点P是BD上一点,且PD=2
 ,一块三角板的直角顶点放在点P上,另两条边与BC、AB所在直线相交于点E、F,在三角板绕点P旋转的过程中,使得△PBF是等腰三角形,(1)线段BD=________,(2)请写出所有满足条件的BF的长__________.
,一块三角板的直角顶点放在点P上,另两条边与BC、AB所在直线相交于点E、F,在三角板绕点P旋转的过程中,使得△PBF是等腰三角形,(1)线段BD=________,(2)请写出所有满足条件的BF的长__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D , CE是△ABC的角平分线.

(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D,E分别是边BC,AC上的点,且BD=EC,∠ADE=∠B.
(1)求证:AD=DE;
(2)若∠ADE=
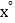 ,求∠ADB的度数(用含x的代数式表示).
,求∠ADB的度数(用含x的代数式表示).
相关试题

