【题目】已知![]() 是
是![]() 的反比例函数,并且当
的反比例函数,并且当![]() 时,
时,![]() .
.
![]() 求
求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
![]() 当
当![]() 时,
时,![]() 的值为________;该函数的图象位于第________象限,在图象的每一支上,
的值为________;该函数的图象位于第________象限,在图象的每一支上,![]() 随
随![]() 的增大而________.
的增大而________.
![]() 直接写出此反比例函数与直线
直接写出此反比例函数与直线![]() 的交点坐标.
的交点坐标.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;一、三;减小.
;一、三;减小.![]() 和
和![]() .
.
【解析】
(1)根据点(2,8)利用待定系数法即可求出反比例函数解析式;
(2)将x=4代入反比例函数解析式中求出y值,再由k=16>0结合反比例函数图象即可得出结论;
(3)联立两函数解析式成方程组,通过解方程组即可求出两函数图象的交点坐标.
(1)设y关于x的函数解析式为y=![]() (k≠0),
(k≠0),
将(2,8)代入y=![]() ,
,
8=![]() ,解得:k=16,
,解得:k=16,
∴y关于x的函数解析式为y=![]() .
.
(2)当x=4时,y=![]() =4;
=4;
∵k=16>0,
∴反比例函数y=![]() 的图象位于第一、三象限,且在图象的每一支上,y随x的增大而减小.
的图象位于第一、三象限,且在图象的每一支上,y随x的增大而减小.
故答案为:4;一、三;减小.
3)联立两函数解析式成方程组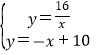 ,
,
解得:![]() ,
,![]() .
.
∴此反比例函数与直线y=x+10的交点坐标为(2,8)和(8,2).
-
科目: 来源: 题型:
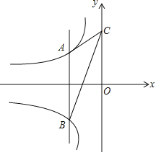
查看答案和解析>>【题目】如图,动点
 在双曲线
在双曲线 上,动点
上,动点 在双曲线
在双曲线 上,且直线
上,且直线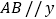 轴,若点
轴,若点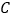 的坐标是
的坐标是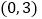 ,点
,点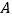 的横坐标为
的横坐标为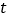 .
.
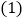 当
当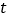 取不同的值时,
取不同的值时,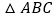 的面积________(填“变化”或者“不变化”);
的面积________(填“变化”或者“不变化”); 线段
线段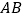 的长可以用
的长可以用 表示为________;
表示为________;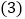 若点
若点 的坐标为
的坐标为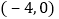 ,请问是否存在常数
,请问是否存在常数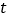 ,使得
,使得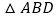 的面积等于
的面积等于 ?若有,请求出
?若有,请求出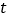 的值;若没有,请说明理由.
的值;若没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
若一个整数能表示成a2+b2(a、b是整数)的形式,则称这个数为“平和数”,例如5是“平和数”,因为5=22+1,再如,M=x2+2xy+2y2=(x+y)2+y2(x, y是整数),我们称M也是“平和数”.
(1)请你写一个小于5的“平和数”,并判断34是否为“平和数”.
(2)已知S=x2+9y2+6x﹣6y+k(x,y是整数,k是常数,要使S为“平和数”,试求出符合条件的一个k值,并说明理由.
(3)如果数m,n都是“平和数”,试说明
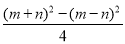 也是“平和数”.
也是“平和数”. -
科目: 来源: 题型:
查看答案和解析>>【题目】先列出下列问题中的函数表达式,再指出它们各属于什么函数.
 电压为
电压为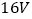 时,电阻
时,电阻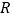 与电流
与电流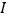 的函数关系;
的函数关系; 食堂每天用煤
食堂每天用煤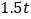 ,用煤总量
,用煤总量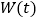 与用煤天数
与用煤天数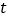 (天)的函数关系;
(天)的函数关系; 积为常数
积为常数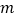 的两个因数
的两个因数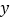 与
与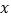 的函数关系;
的函数关系; 杠杆平衡时,阻力为
杠杆平衡时,阻力为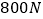 ,阻力臂长为
,阻力臂长为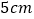 ,动力
,动力 与动力臂
与动力臂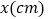 的函数关系(杠杆本
的函数关系(杠杆本身所受重力不计).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD为△ABC的角平分线,CE为△ABC的高,CE 交BD于点F,∠A=80°,∠BCA=50°,那么∠BFC的度数是( ).

A.115°B.120°C.125°D.130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,CE和BD交于点O,AO的延长线交BC于点F,则图中全等的三角形有( )

A.8对B.7对C.6对D.5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 点
点 关于
关于 轴对称的点的坐标是________.
轴对称的点的坐标是________. 反比例函数
反比例函数 关于
关于 轴对称的函数的解析式为________.
轴对称的函数的解析式为________. 求反比例函数
求反比例函数 关于
关于 轴对称的函数的解析式.
轴对称的函数的解析式.
相关试题

