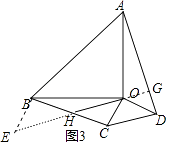
【题目】已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.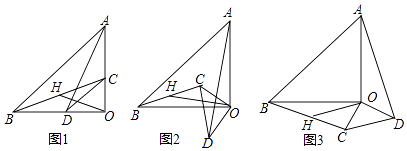
(1)如图1所示,易证:OH= ![]() AD且OH⊥AD(不需证明)
AD且OH⊥AD(不需证明)
(2)将△COD绕点O旋转到图2,图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论.
参考答案:
【答案】
(1)证明:如图1中,
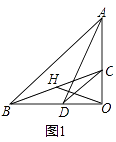
∵△OAB与△OCD为等腰直角三角形,∠AOB=∠COD=90°,
∴OC=OD,OA=OB,
∵在△AOD与△BOC中,
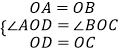 ,
,
∴△AOD≌△BOC(SAS),
∴∠ADO=∠BCO,∠OAD=∠OBC,
∵点H为线段BC的中点,
∴OH=HB,
∴∠OBH=∠HOB=∠OAD,
又因为∠OAD+∠ADO=90°,
所以∠ADO+∠BOH=90°,
所以OH⊥AD
(2)解:①结论:OH= ![]() AD,OH⊥AD,如图2中,延长OH到E,使得HE=OH,连接BE,
AD,OH⊥AD,如图2中,延长OH到E,使得HE=OH,连接BE,
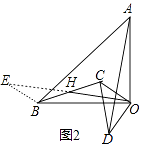
易证△BEO≌△ODA
∴OE=AD
∴OH= ![]() OE=
OE= ![]() AD
AD
由△BEO≌△ODA,知∠EOB=∠DAO
∴∠DAO+∠AOH=∠EOB+∠AOH=90°,
∴OH⊥AD.
②如图3中,结论不变.延长OH到E,使得HE=OH,连接BE,延长EO交AD于G.
易证△BEO≌△ODA
∴OE=AD
∴OH= ![]() OE=
OE= ![]() AD
AD
由△BEO≌△ODA,知∠EOB=∠DAO
∴∠DAO+∠AOF=∠EOB+∠AOG=90°,
∴∠AGO=90°
∴OH⊥AD.
【解析】(2)利用第1题的解题方法,要证OH= ![]() AD即AD=2OH,因此须延长OH一倍,连结BE,构造全等三角形△BEO≌△ODA即可证得.
AD即AD=2OH,因此须延长OH一倍,连结BE,构造全等三角形△BEO≌△ODA即可证得.
【考点精析】通过灵活运用等腰直角三角形和旋转的性质,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.
-
科目: 来源: 题型:
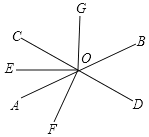
查看答案和解析>>【题目】如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
(1)求∠AOC,∠AOF的度数;
(2)求∠EOF与∠BOG是否相等?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC.

(1)求证:DE是圆O的切线;
(2)若∠C=30°,CD=10cm,求圆O的半径. -
科目: 来源: 题型:
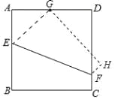
查看答案和解析>>【题目】如图,将边长为4的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处.
(1)求线段BE的长;
(2)连接BF、GF,求证:BF=GF;
(3)求四边形BCFE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了推动“龙江经济带”建设,我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展.2017年春,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元/公顷,青椒1.5万元/公顷,马铃薯2万元/公顷,设种植西红柿x公顷,总利润为y万元.
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式.
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?
(3)在(2)的前提下,该企业决定投资不超过获得最大利润的 在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC经过平移后得到△DEF,点A与点D,点B与点E,点C与点F分别是对应点,已知点A(3,3)、D(-2,1),解答下列问题:
(1)请在坐标系中画出平移后的△DEF;
(2)请直接写出以下点的坐标:B(___,___)、C(___,___)、E(___,___)、F(___,___);
(3)若点P(x,y)通过上述的平移规律平移得到的对应点为Q(3,5),则P点坐标为(____,____).

-
科目: 来源: 题型:
查看答案和解析>>【题目】小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明(包含设计费与印刷费),乙公司的收费与印刷卡片数量的关系如图2所示.
(1)分别写出甲乙两公司的收费y(元)与印刷数量x之间的关系式.
(2)如果你是小强,你会选择哪家公司?并说明理由.

相关试题

