【题目】如图,在正方形网格上有一个△DEF.
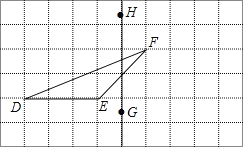
(1)画出△DEF关于直线HG的轴对称图形(不写画法);
(2)画EF边上的高(不写画法);
(3)若网格上的最小正方形边长为1,则△DEF的面积为 .
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)3
【解析】
(1)根据网格结构找出点D、E、F关于直线HG的对称点D′、E′、F′的位置,然后顺次连接即可;
(2)根据网格结构以及EF的位置,过点D作小正方形的对角线,与FE的延长线相交于H,DH即为所求作的高线;
(3)DE为底边,点F到DE的距离为高,根据三角形的面积公式列式进行计算即可得解.
解:(1)如图所示,△D′E′F′即为所求作的△DEF关于直线HG的轴对称图形;
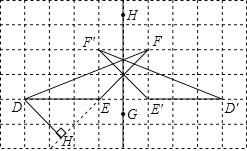
(2)如图所示,DH为EF边上的高线;
(3)△DEF的面积=![]() ×3×2=3.
×3×2=3.
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
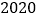 年是我国实现第一个百年目标,全国建成小康社会的收官之年,早在十六大我党就提出加快推进社会主义现代化,力争国民生产总值到
年是我国实现第一个百年目标,全国建成小康社会的收官之年,早在十六大我党就提出加快推进社会主义现代化,力争国民生产总值到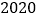 年比
年比 年翻两番,要实现这一目标,以十年为单位计算,求每十年的国民生产总值的增长率是多少?
年翻两番,要实现这一目标,以十年为单位计算,求每十年的国民生产总值的增长率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBA和△EDC一定是全等三角形;②△EBD是等腰三角形,EB=ED;③折叠后得到的图形是轴对称图形;④折叠后∠ABE和∠CBD一定相等;其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠BAD=100°,∠B=∠D=90°,在BC、CD上分别找一个点M、N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )

A.130°B.120°C.160°D.100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在△ABC和△AEF中,点E在BC边上,AE=AB,AC=AF,∠CAF=∠BAE,EF与AC交于点G.

(1)求证:EF=BC;
(2)若∠ABC=65°.∠ACB=28°,求∠FGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学八年级(5)班的学生到野外进行数学活动,为了测量一池塘两端A、B之间的距离,同学们设计了如下两种方案:
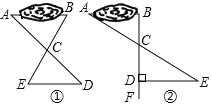
方案1:如图(1),先在平地上取一个可以直接到达A、B的点C,连接AC并延长AC至点D,连接BC并延长至点E,使DC=AC,EC=BC,最后量出DE的距离就是AB的长.
方案2:如图(2),过点B作AB的垂线BF,在BF上取C、D两点,使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB间的距离
问:(1)方案1是否可行?并说明理由;
(2)方案2是否可行?并说明理由;
(3)小明说:“在方案2中,并不一定需要BF⊥AB,DE⊥BF,将“BF⊥AB,DE⊥BF”换成条 也可以.”你认为小明的说法正确吗?如果正确的话,请你把小明所说的条件补上.
相关试题

