【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.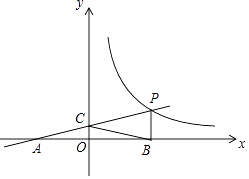
(1)求一次函数,反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
参考答案:
【答案】
(1)
解:∵点A与点B关于y轴对称,
∴AO=BO,
∵A(﹣4,0),
∴B(4,0),
∵PB⊥x轴于点B,
∴P(4,2),
把P(4,2)代入反比例函数解析式可得m=8,
∴反比例函数解析式为y= ![]() ,
,
把A、P两点坐标代入一次函数解析式可得 ![]() ,解得
,解得 ![]() ,
,
∴一次函数解析式为y= ![]() x+1
x+1
(2)
证:∵点A与点B关于y轴对称,
∴OA=OB,
∵PB⊥x轴于点B,
∴∠PBA=∠COA=90°,
∴PB∥CO,
∴ ![]() =
= ![]() =1,即AC=PC,
=1,即AC=PC,
∴点C为线段AP的中点
(3)
解:存在点D,使四边形BCPD为菱形.
理由如下:
∵点C为线段AP的中点,
∴BC= ![]() AP=PC,
AP=PC,
∴BC和PC是菱形的两条边,
由y= ![]() x+1可得C(0,1),
x+1可得C(0,1),
如图,过点C作CD∥x轴,交PB于点E,交反比例函数图象于点D,分别连接PD、BD,
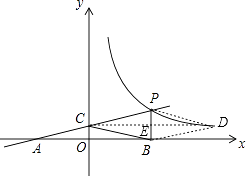
∴D(8,1),且PB⊥CD,
∴PE=BE=1,CE=DE=4,
∴PB与CD互相垂直平分,即四边形BCPD为菱形,
∴存在满足条件的点D,其坐标为(8,1)
【解析】(1)由条件可求得P点坐标,利用待定系数法可求得一次函数和反比例函数的解析式;(2)由平行线分线段成比例可求得AC=PC,可证得结论;(3)可先求得C点坐标,过C作CD∥x轴,交PB于点E,交反比例函数图象于点D,可求得此时D点坐标,可证得四边形BCPD为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
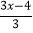 -
-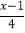 =1-
=1-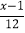
解:去分母,得_________________________________.
去括号,得___________________________.
移项,得___________________________.
合并同类项,得__________.
两边都除以______,得x=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
国际比赛的足球场长在100m到110m之间,宽在64m到75m之间,为了迎接2015年的亚洲杯,某地建设了一个长方形的足球场,其长是宽的1.5倍,面积是7560m2.请你判断这个足球场能用于国际比赛吗?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点 A1、A2、A3、…在射线 ON 上,点 B1、B2、B3、…在射线 OM 上;△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形.若 OA1=1,则△A2015B2015A2016 的边长为 ( )
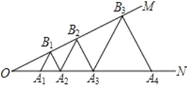
A. 4028 B. 4030 C. 22014 D. 22015
-
科目: 来源: 题型:
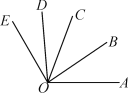
查看答案和解析>>【题目】如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOC=70°,∠COE=50°,那么∠BOD是多少度?
(2)如果∠BOD=70°,那么∠AOE是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ABCD 中,AB⊥AD,BC⊥DC,点 M、N 分别是 AB、BC 边上的动点,∠B=56°.当△DMN 的周长最小时,则∠MDN 的度数是_____

相关试题

