【题目】.A,B,C为数轴上三点,若点C到点A的距离是点C到点B的距离的2倍,我们就称点C是【A,B】的和谐点.例如:图1中,点A表示的数为-1,点B表示的数为2。表示1的点C到点A的距离是2,到点B的距离是1.那么点C是【A,B】的和谐点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是【A,B】的和谐点,但点D是【B,A】的和谐点
(1)若数轴上M,N两点所表示的数分别为![]() 且
且![]() 满足
满足![]() ,请求
,请求
出【M,N】的和谐点表示的数;
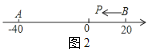
(2)如图2,A,B在数轴上表乐的数分别为-40和20,现有一点P从点B出发向左运动
①若点P到达点A停止,则当P点运动多少个单位时P,A,B中恰有一个点为其余两点的和谐点?
②若点P到达点A后继续向左运动,是否存在使得P,A,B中恰有一个点为其余两点的和谐点的情况?若存在,请直接写出此时PB的距离,若不存在,请说明理由.

参考答案:
【答案】见解析
【解析】试题分析:(1)由题意得出m=-2,n=4,设【M、N】的和谐点表示的数为x,根据和谐点的定义可列方程x-(-2)=2(4-x),解出x=2;(2)①分四种情况讨论,1.P是【A、B】的和谐点;2.P是【B、A】是和谐点; 3.B是【A、P】的和谐点;4.A为【B、P】的和谐点,分别列出方程解出y,计算出P点运动的单位即可;②分四种情况讨论:1.当点P是【B、A】的和谐点,2.当点A是【P、B】的和谐点,3.当点A是【B、P】的和谐点,4.当点B是【P、A】的和谐点,分别计算出PB即可.
试题解析:
解:(1)由题意得:m=-2,n=4,
设【M、N】的和谐点表示的数为x,
∴x-(-2)=2(4-x),x=2.
∴【M、N】的和谐点表示的数为2;
(2)①设点P表示的数为y,分四种情况:
1.P是【A、B】的和谐点,
由题意,得y-(-40)=2(20-y),
解得y=0,
20-0=20;
2.P是【B、A】是和谐点,
由题意,得20-y=2[y-(-40)],
解得y=-20,
20-(-20)=40;
3.B是【A、P】的和谐点,
由题意,得20-(-40)=2(20-y),
解得y=-10,
20-(-10)=30;
4.A为【B、P】 的和谐点,
由题意,得20-(-40)=2[y-(-40)],
解得y=-10,
20-(-10)=30.
综上可知,当P点运动20或40或30个单位时,P、A和B中恰有一个点为其余两点的和谐点.
(3)当点P是【B、A】的和谐点,PB=120;
当点A是【P、B】的和谐点,PB=180;
当点A是【B、P】的和谐点,PB=90;
当点B是【P、A】的和谐点,PB=120.
综上,PB距离为80或120或180时,P、A、B中恰有一个点为其余两点的和谐点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个样本中,50个数据分别落在5个组内,第一、二、三、四、五组数据的个数分别为2、8、15、20、5,则第四组的频率为( )
A.0.1
B.0.2
C.0.3
D.0.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】有一个样本有100个数据,落在某一组内的频率是0.3,那么落在这一组内的频数是( )
A.50
B.30
C.15
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】若用反证法证明“三个内角不相等的三角形不是等腰三角形”,可先假设这个三角形是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
 与正比例函数y=ax相交于A(1,k),B(-k,-1)两点。
与正比例函数y=ax相交于A(1,k),B(-k,-1)两点。(1)求反比例函数和正比例函数的解析式;
(2)将正比例函数y=ax的图象平移,得到一次函数y=ax+b的图象,与函数
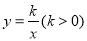 的图象交于C(x1,y1)、D(x2,y2),且|x1-x2|·|y1-y2|=5,求b的值。
的图象交于C(x1,y1)、D(x2,y2),且|x1-x2|·|y1-y2|=5,求b的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣2x2﹣4x+1,当﹣3≤x≤2时,则函数值y的最小值为( )
A.﹣15B.﹣5C.1D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】威远人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,两种牛奶的总数不超过95件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)超过371元,请通过计算求出该商场购进甲、乙两种牛奶有哪几种方案?
相关试题

